Предмет: Алгебра,
автор: krasi446
помогите решить логгарифмическое неравенство!
Приложения:
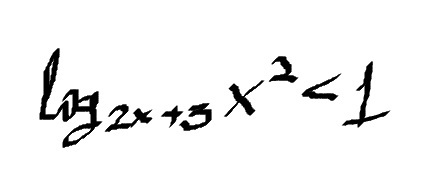
Ответы
Автор ответа:
0
1 = log2x+3(2x+3)
наш пример:
log2x+3(x²) < log2x+3(2x +3)
a) 2x +3 > 1, x > -1
x² < 2x +3,⇒ x² -2x -3 <0, ⇒ x∈(-1;3)
ОДЗ х²> 0 ( при любом х)
Ответ:(-1;3)
б) 0 < 2х +3 <1 ,⇒ -1,5 < x < -1
x² > 2x +3 , ⇒ x∈(-∞; -1) ∪ (3; +∞)
наш пример:
log2x+3(x²) < log2x+3(2x +3)
a) 2x +3 > 1, x > -1
x² < 2x +3,⇒ x² -2x -3 <0, ⇒ x∈(-1;3)
ОДЗ х²> 0 ( при любом х)
Ответ:(-1;3)
б) 0 < 2х +3 <1 ,⇒ -1,5 < x < -1
x² > 2x +3 , ⇒ x∈(-∞; -1) ∪ (3; +∞)
Похожие вопросы
Предмет: Алгебра,
автор: Pamagitiiiiimene
Предмет: Литература,
автор: Аноним
Предмет: История,
автор: gafatullink
Предмет: Математика,
автор: evakapitonova
Предмет: Математика,
автор: Trikoyach