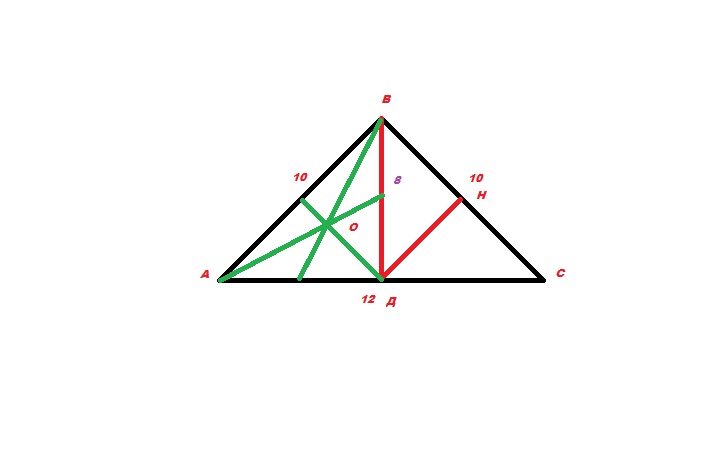
Построить треугольник ABC со сторонами: AB-10см, BC-10см, AC-12см. Провести высоту BD, разделившую данный треугольник на 2 треугольника. В треугольнике BDC построить высоту DH и вычислить длинну. В треугольнике ABD найти длинну AO, O-точка пересечения медиан. Вычеслить периметры и площади этих треугольников. Запишите решение построения треугольников. Решите на листке и сфотографируйте реш
Ответы
решение во вложениях
,,,,,,,,,,,,,


Дано:
АВ - 10
ВС - 10
АС - 10
ВД- высота
Найти:
ДН - ?
АО - ?
Р - ?
S - ?
Решение:
ВД=√(10²-(12/2)²)=√(100-36)=√64=8
периметр АВС = 10+10+12=32
площадь АВС = 10*10/2=50
периметр АВД и ВДС = 10+6+8=24
площадь АВД и ВДС = 8*6/2=24
ДМ медиана, она равна половине гипотенузы, по теореме:
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности, отсюда получам, что ДМ=10/2=5
ДО можно вычислить по формуле: r=(a*b)/(a+b+c)=8*6/24=2.
DH найдём по формуле h=ab/c=8*6/10=4.8