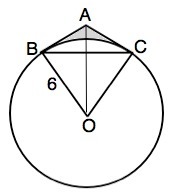
очень нужно))из точки А к окр. с центром О и радиусом,равным 6 см проведены две касательные АВ и АС образующие между собой угол в 120 градусов . Найдите периметр и площадь фигуры ограниченной отрезками АВ иАС и дугой ВС окружности, если центр окружности не содержится во внутренней области полученной фигуры.
Ответы
Искомую площадь можно найти по-разному.
1) Найти площадь четырехугольника АВОС и из нее вычесть площадь сектора круга.
2) Найти площадь ∆ АВС и из неё вычесть площадь сегмента. ограниченного дугой ВС и хордой ВС.
1) Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности⇒
∠ВАО=∠САО=120°:2=60°
∠АВО=∠АСО=90° т.к. радиусы, проведенные в точки касания, перпендикулярны касательным. ⇒
угол ВОС=60°, и ∆ ВОС - равносторонний.
∆ АВО=∆ АСО - прямоугольные.
АВ=BО:tg60°=6/√3=2√3
Длина дуги ВС =1/6 длины окружности, т.к. угол ВОС=1/6 полного круга.
◡ВС=2πr:6=12π:6=2π
P=AB+AC+◡BC=2•2√3+2π=4√3+2π = ≈13,2114 см
----------------
Ѕ (АВОС)=2Ѕ(АВО)=ВО•AB=6•2√3=12√3
S (сектора)=1/6πr²=36π:6=6π
S(фиг. АВС)=S(ABOC)-S(сект)=12√3-6π=6•(2√3-π)=≈1,935 см*
2) По второму способу попробуйте вычислить искомую площадь самостоятельно. Результат получится тот же, что найденная по первому способу.