Предмет: Алгебра,
автор: nikitabuynokiax
2) помогите, пожалуйста
Приложения:
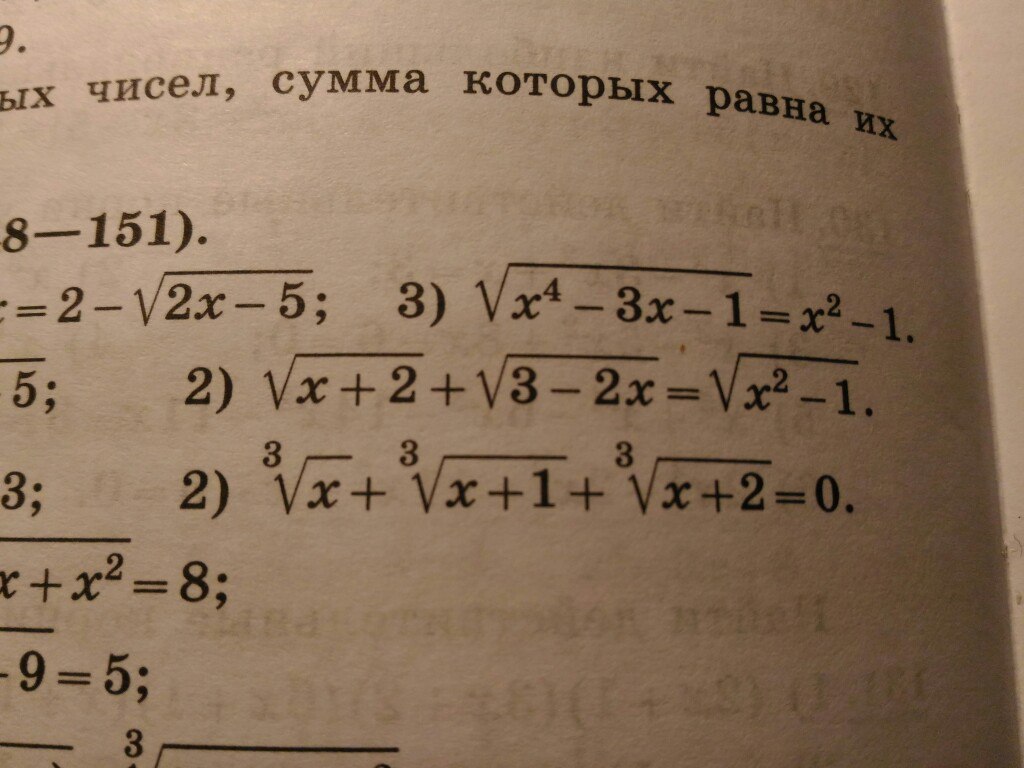
Ответы
Автор ответа:
0
Решение смотри в приложении
Приложения:


Автор ответа:
0
* ДЛЯ ИНТЕРЕСУЮЩИХСЯ ВЫСШЕЙ МАТЕМАТИКОЙ
** Самое решение через граничные условия размещено на изображении.
Строго говоря, с точки зрения высшей математики, приведённое в пункте 2) куб-радикальное уравнение не имеет решений, что мы подробно обсудили с Владимиром Б. Так, если это уравнение решать в известной математической системе Wolfram, то система сообщит, что «решений нет».
[ u . to / eL4zDg ] (ссылка, уберите пробелы) . Выясним, почему это так.
В школьной математике мы вводим такое понятие, как «арифметический квадратный корень». Это ОДНОЗНАЧНАЯ арифметическая операция, приводящая к одному числу. Так, например:
 ,
,
и .
.
В высшей алгебре используется понятие «алгебраический квадратный корень». Это НЕОДНОЗНАЧНОЕ, а именно ДВУХЗНАЧНОЕ действие, приводящее сразу к МНОЖЕСТВУ, т.е. к ПАРЕ значений, так что:
![sqrt[2]{4} = pm 2 sqrt[2]{4} = pm 2](https://tex.z-dn.net/?f=+sqrt%5B2%5D%7B4%7D+%3D+pm+2+) ,
,
и![sqrt[2]{5} = pm sqrt{5} sqrt[2]{5} = pm sqrt{5}](https://tex.z-dn.net/?f=+sqrt%5B2%5D%7B5%7D+%3D+pm+sqrt%7B5%7D+) (во втором случае множество значений алгебраического корня выражено через арифметический корень).
(во втором случае множество значений алгебраического корня выражено через арифметический корень).
Аналогично, в школьной математике умалчивается, что кубический корень – это НЕОДНОЗНАЧНОЕ, а именно ТРЁХЗНАЧНОЕ действие, приводящее сразу к МНОЖЕСТВУ, т.е. к ТРОЙКЕ значений, так что:
![sqrt[3]{8} in { 2, [ -1 + isqrt{3} ] , [ -1 - isqrt{3} ] } sqrt[3]{8} in { 2, [ -1 + isqrt{3} ] , [ -1 - isqrt{3} ] }](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B8%7D+in+%7B+2%2C+%5B+-1+%2B+isqrt%7B3%7D+%5D+%2C+%5B+-1+-+isqrt%7B3%7D+%5D+%7D+) ,
,
и![sqrt[3]{-8} in { [ 1 + isqrt{3} ] , -2, [ 1 - isqrt{3} ] } sqrt[3]{-8} in { [ 1 + isqrt{3} ] , -2, [ 1 - isqrt{3} ] }](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B-8%7D+in+%7B+%5B+1+%2B+isqrt%7B3%7D+%5D+%2C+-2%2C+%5B+1+-+isqrt%7B3%7D+%5D+%7D+) ;
;
Если вы не знакомы с понятием комплексных чисел вида![[ 1 + isqrt{3} ] , [ 1 + isqrt{3} ] ,](https://tex.z-dn.net/?f=+%5B+1+%2B+isqrt%7B3%7D+%5D+%2C+) которые изучают только в школьных спецкурсах и в институтах, то просто пропустите следующие два абзаца со звёздочкой * , и просто примите к сведению, что есть такие числа – комплексные. Если же вы, хоть немного знакомы с ними – то докажем, что приведённые значения кубических корней верны.
которые изучают только в школьных спецкурсах и в институтах, то просто пропустите следующие два абзаца со звёздочкой * , и просто примите к сведению, что есть такие числа – комплексные. Если же вы, хоть немного знакомы с ними – то докажем, что приведённые значения кубических корней верны.
*


* аналогично можно показать, что и остальные значения в фигурных скобках, при возведении их в куб будут равны или
или  – соответственно.
– соответственно.
Кстати, всем известные «действительные», или «вещественные» числа – являются подмножеством (частным случаем) комплексных чисел (с нулевой мнимой частью). Не нужно «отвергать» понятие мнимых и комплексных чисел, как что-то ненужное, запутанное и фантазийное, что придумывают «умные дяди в математических институтах». Это очень даже нужные числа, которые повсеместно используются и в физике, и в электротехнике, и в аудио- видео- электронике, и в экономике, да и в самой математике, когда через мнимые числа находятся вещественные.
У корней, кроме их значений, существует и такое понятие, как кратность. У алгебраического квадратного корня кратность равна либо нулю (это положительные значения), либо единице (это отрицательные значения). У кубического корня кратность может быть равна: 0, 1 или 2. Корни с кратностью 0 (ноль) – называются главными корнями.
Теперь запишем всё точно:
Кубический корень нулевой кратности из 1 :![sqrt[3]{1} = 1 sqrt[3]{1} = 1](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B1%7D+%3D+1+) ,
,
Кубический корень 1-ой кратности из 1 :![sqrt[3]{1} = frac{ -1 + isqrt{3} }{2} sqrt[3]{1} = frac{ -1 + isqrt{3} }{2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B1%7D+%3D+frac%7B+-1+%2B+isqrt%7B3%7D+%7D%7B2%7D+) ,
,
Кубический корень 2-ой кратности из 1 :![sqrt[3]{1} = frac{ -1 - isqrt{3} }{2} sqrt[3]{1} = frac{ -1 - isqrt{3} }{2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B1%7D+%3D+frac%7B+-1+-+isqrt%7B3%7D+%7D%7B2%7D+) ,
,
Кубический корень нулевой кратности из (-1) :![sqrt[3]{-1} = frac{ 1 + isqrt{3} }{2} sqrt[3]{-1} = frac{ 1 + isqrt{3} }{2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B-1%7D+%3D+frac%7B+1+%2B+isqrt%7B3%7D+%7D%7B2%7D+) ,
,
Кубический корень 1-ой кратности из (-1) :![sqrt[3]{1} = -1 sqrt[3]{1} = -1](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B1%7D+%3D+-1+) ,
,
Кубический корень 2-ой кратности из (-1) :![sqrt[3]{1} = frac{ 1 - isqrt{3} }{2} sqrt[3]{1} = frac{ 1 - isqrt{3} }{2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B1%7D+%3D+frac%7B+1+-+isqrt%7B3%7D+%7D%7B2%7D+) ,
,
Итак, главные корни:
![sqrt[3]{1} = 1 sqrt[3]{1} = 1](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B1%7D+%3D+1+) ,
,
![sqrt[3]{-1} = frac{ 1 + isqrt{3} }{2} sqrt[3]{-1} = frac{ 1 + isqrt{3} }{2}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B-1%7D+%3D+frac%7B+1+%2B+isqrt%7B3%7D+%7D%7B2%7D+) .
.
Откуда следует. что если в заданное в условии уравнение подставить значение то мы, с точки зрения высшей алгебры, получим неверное равенство:
то мы, с точки зрения высшей алгебры, получим неверное равенство:
![sqrt[3]{-1} + sqrt[3]{0} + sqrt[3]{1} = frac{ 3 + isqrt{3} }{2} neq 0 sqrt[3]{-1} + sqrt[3]{0} + sqrt[3]{1} = frac{ 3 + isqrt{3} }{2} neq 0](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B-1%7D+%2B+sqrt%5B3%5D%7B0%7D+%2B+sqrt%5B3%5D%7B1%7D+%3D+frac%7B+3+%2B+isqrt%7B3%7D+%7D%7B2%7D+neq+0+) .
.
Аналогично, верное тождество не получается и при использовании кубических корней 1-ой или 2-ой кратности для значения
** Самое решение через граничные условия размещено на изображении.
Строго говоря, с точки зрения высшей математики, приведённое в пункте 2) куб-радикальное уравнение не имеет решений, что мы подробно обсудили с Владимиром Б. Так, если это уравнение решать в известной математической системе Wolfram, то система сообщит, что «решений нет».
[ u . to / eL4zDg ] (ссылка, уберите пробелы) . Выясним, почему это так.
В школьной математике мы вводим такое понятие, как «арифметический квадратный корень». Это ОДНОЗНАЧНАЯ арифметическая операция, приводящая к одному числу. Так, например:
и
В высшей алгебре используется понятие «алгебраический квадратный корень». Это НЕОДНОЗНАЧНОЕ, а именно ДВУХЗНАЧНОЕ действие, приводящее сразу к МНОЖЕСТВУ, т.е. к ПАРЕ значений, так что:
и
Аналогично, в школьной математике умалчивается, что кубический корень – это НЕОДНОЗНАЧНОЕ, а именно ТРЁХЗНАЧНОЕ действие, приводящее сразу к МНОЖЕСТВУ, т.е. к ТРОЙКЕ значений, так что:
и
Если вы не знакомы с понятием комплексных чисел вида
*
* аналогично можно показать, что и остальные значения в фигурных скобках, при возведении их в куб будут равны
Кстати, всем известные «действительные», или «вещественные» числа – являются подмножеством (частным случаем) комплексных чисел (с нулевой мнимой частью). Не нужно «отвергать» понятие мнимых и комплексных чисел, как что-то ненужное, запутанное и фантазийное, что придумывают «умные дяди в математических институтах». Это очень даже нужные числа, которые повсеместно используются и в физике, и в электротехнике, и в аудио- видео- электронике, и в экономике, да и в самой математике, когда через мнимые числа находятся вещественные.
У корней, кроме их значений, существует и такое понятие, как кратность. У алгебраического квадратного корня кратность равна либо нулю (это положительные значения), либо единице (это отрицательные значения). У кубического корня кратность может быть равна: 0, 1 или 2. Корни с кратностью 0 (ноль) – называются главными корнями.
Теперь запишем всё точно:
Кубический корень нулевой кратности из 1 :
Кубический корень 1-ой кратности из 1 :
Кубический корень 2-ой кратности из 1 :
Кубический корень нулевой кратности из (-1) :
Кубический корень 1-ой кратности из (-1) :
Кубический корень 2-ой кратности из (-1) :
Итак, главные корни:
Откуда следует. что если в заданное в условии уравнение подставить значение
Аналогично, верное тождество не получается и при использовании кубических корней 1-ой или 2-ой кратности для значения
Приложения:

Похожие вопросы
Предмет: География,
автор: bisenovaelnara160
Предмет: Русский язык,
автор: ermekmadi77
Предмет: Математика,
автор: alimamedov08
Предмет: Математика,
автор: Яхочуспать