Решите номер 1.Есть вложение.По плану.

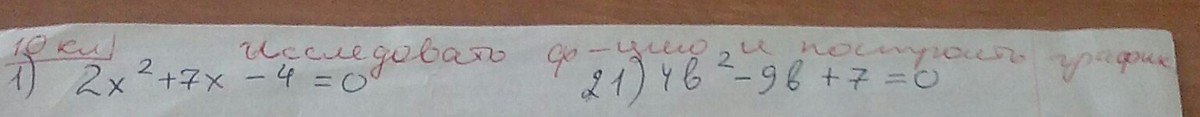
Ответы
1) Область определения функции.
Полиномиальная функция без корней или переменных в знаменателе.
Для этого типа функции область определения - все действительные числа.
x ∈ (-∞; +∞).
2) Производная функции равна:
f ' = 4x + 7.
3) Производная функции равна нулю в точке:
4х + 7 = 0
х = -7/4 = -1,75.
Эта точка соответствует вершине параболы.
5) Так как коэффициент при х² положителен то ветви параболы направлены вверх.
Поэтому у параболы нет максимума, а есть только минимум.
Минимум находится в вершине параболы:
хо найдено и равно -1,75.
Минимум функции уо=2*(-7/4)²+7*(-7/4)-4 = 2*(49/16)-(49/4)-4 = (98-196-64)/16 = -162/16 = -81/8 = -10,125.
6) Нули функции соответствуют точкам пересечения параболы с осью х, при этом у=0.
2х²+7х-4 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=7^2-4*2*(-4)=49-4*2*(-4)=49-8*(-4)=49-(-8*4)=49-(-32)=49+32=81;
Дискриминант больше 0, уравнение имеет 2 корня:
x1=(√81-7)/(2*2)=(9-7)/(2*2)=2/(2*2)=2/4=0.5;
x2=(-√81-7)/(2*2)=(-9-7)/(2*2)=-16/(2*2)=-16/4=-4.
то есть точки х = 0,5 и
х = -4.
7) Точка пересечения с осью ординат соответствует значению х = 0, в данной точке функция равна -4.
8) График и таблица точек для его построения приведен в приложении.