Предмет: Алгебра,
автор: Аноним
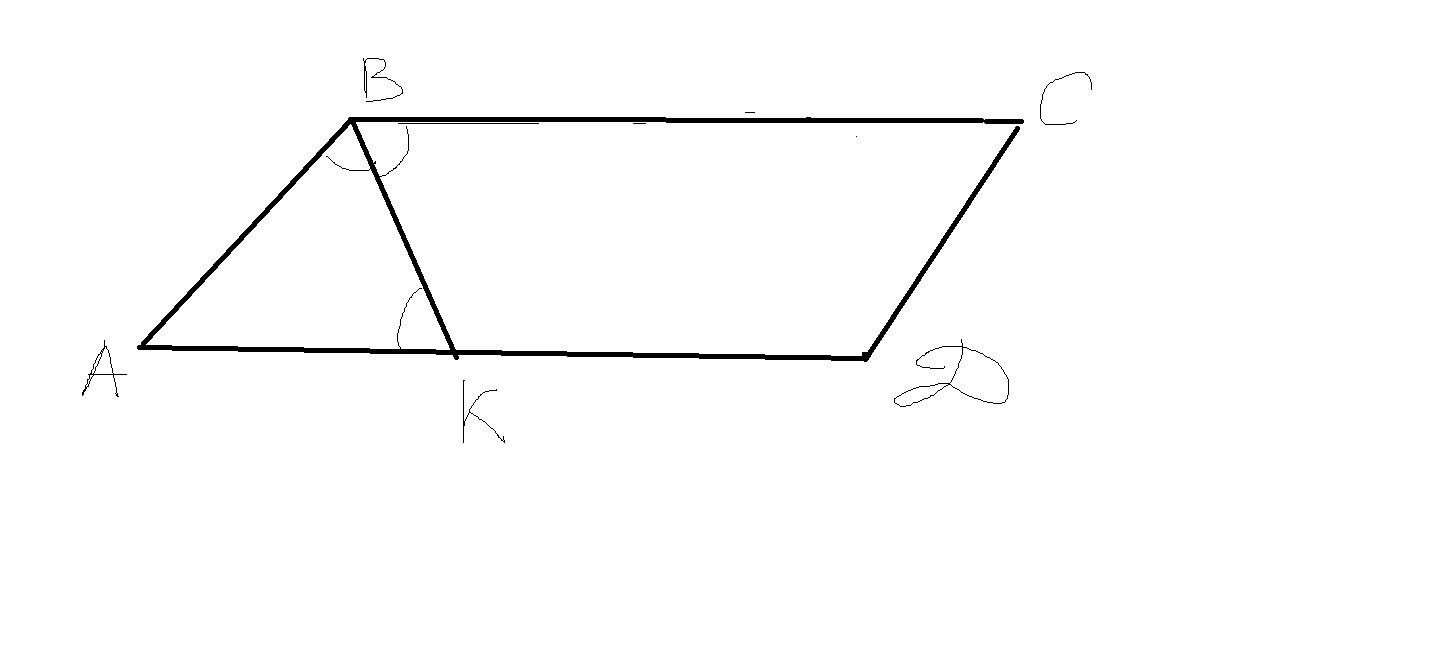
Биссектриса тупого угла B параллелограмма ABCD делит сторону AD в
отношении 1:3, считая от вершины A. Найдите сторону AB, если
полупериметр параллелограмма равен 55.
Ответы
Автор ответа:
0
Ответ: 11.
Пошаговое объяснение:
Биссектриса угла В делит угол пополам, т.е. ∠ABK = ∠CBK.
∠CBK = ∠BKA как накрест лежащие при AD || BC и секущей ВК
Так как ∠ABK = ∠BKA , то ΔABK — равнобедренный; AB = AK.
Пусть коэффициент пропорциональности равен х, тогда AK = x; DK=3x; AD=x+3x=4x. Периметр параллелограмма: P = x + x + 4x + 4x = 10x
Из условия полупериметр параллелограмма = 55, тогда Р=2*55=110
10x = 110
x = 11 — сторона АВ.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: albinatursynov
Предмет: Другие предметы,
автор: innavalujskaa802
Предмет: Русский язык,
автор: cvngcbhdfb
Предмет: Обществознание,
автор: Аaлекc
Предмет: Математика,
автор: slava61