Question

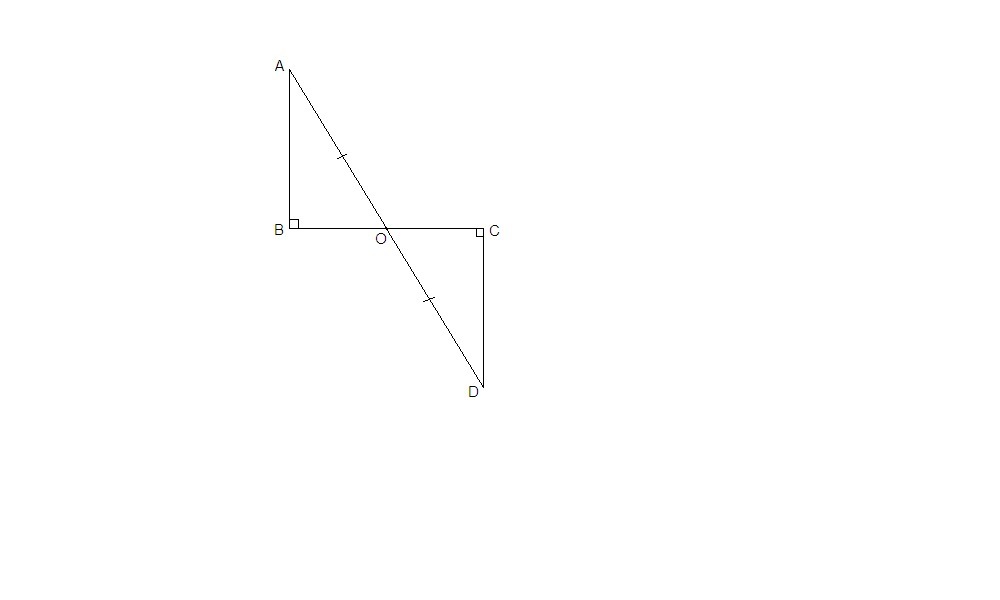
На рисунке: угол B=углу C=90°.AO=OD. Докажите,что ∆ABO=∆OCD,и найдите угол A,если угол D=38°

Answer 1

AB║CD как два перпендикуляра к одной прямой (АВ⊥ВС и CD⊥BC), значит
∠ВАО = ∠CDO как накрест лежащие при пересечении параллельных прямых АВ и CD секущей AD.
АО = OD по условию,
∠АОВ = ∠DOC как вертикальные, ⇒
ΔАОВ = ΔDOC по стороне и двум прилежащим к ней углам.
Из равенства треугольников следует, что
∠ВАО = ∠CDO = 38°.