Предмет: Геометрия,
автор: Funn2ybunndanam
Даю много баллов!!!!!!
Площадь треугольника АВС равна 1. На сторонах АВ, ВС, СА, взяты соответственно
точки А1, В1, С1 так, что АА1 : А1В = 1:2, ВВ1 : В1С = 1:3, точка С1 делит сторону АС
пополам. Найдите площадь треугольника А1В1С1.
Ответы
Автор ответа:
0
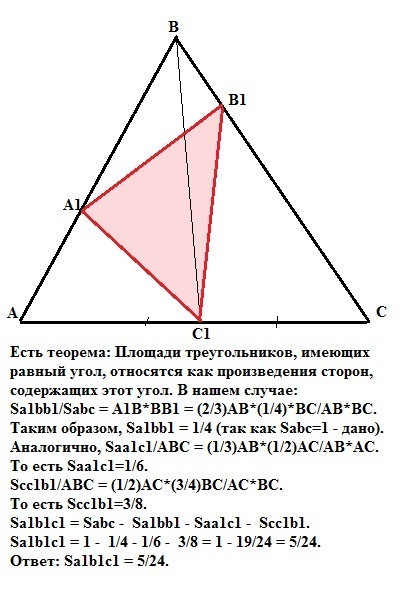
Есть теорема: Площади треугольников, имеющих равный угол, относятся как произведения сторон, содержащих этот угол. В нашем случае:
Sa1bb1/Sabc = A1B*BB1 = (2/3)AB*(1/4)*BC/AB*BC.
Таким образом, Sa1bb1 = 1/4 (так как Sabc=1 - дано).
Аналогично, Saa1c1/ABC = (1/3)AB*(1/2)АС/АВ*АС.
То есть Saa1c1=1/6.
Scc1b1/ABC = (1/2)AC*(3/4)BC/АC*BС.
То есть Scc1b1=3/8.
Sa1b1c1 = Sabc - Sa1bb1 - Saa1c1 - Scc1b1.
Sa1b1c1 = 1 - 1/4 - 1/6 - 3/8 = 1 - 19/24 = 5/24.
Ответ: Sa1b1c1 = 5/24.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: maximshekshaev
Предмет: Английский язык,
автор: KiraLoovegood
Предмет: Математика,
автор: llerchek
Предмет: Алгебра,
автор: zavalishina
Предмет: Алгебра,
автор: Dizfanit