Question

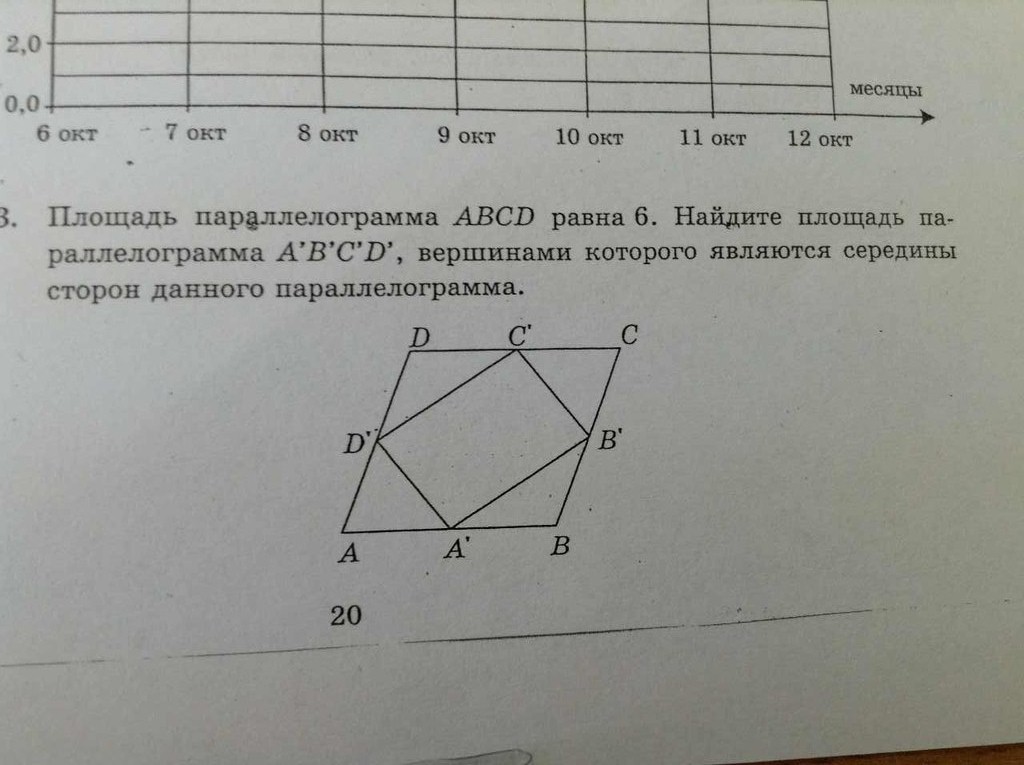
Площадь параллелограмма ABCD равна 6. Найдите площадь параллелограмма A'B'C'D', вершинами которого являются середины сторон данного параллелограмма (Картинка)

Answer 1

Площадь параллелограмма D'DCB' равна половине площади параллелограмма ADCB, так как D'B' соединяет середины сторон AD и CB. Площадь треугольника D'C'B' равна половине параллелограмма D'DCB', так как имеют общее основание и высоту.
Итак, треугольник D'C'B' равен 3/2.
Площадь параллелограмма A'D'C'B' равна двум площадям треугольника D'C'B', так как треугольник A'D'B' равен треугольнику D'C'B'.
Следовательно, площадь параллелограмма A'D'C'B' = 2*(3/2)=3.