Предмет: Математика,
автор: Forever101
Помогите пожалуйста! Дайте ответ с решением! Математика 11 класс. Спасибо.
Приложения:
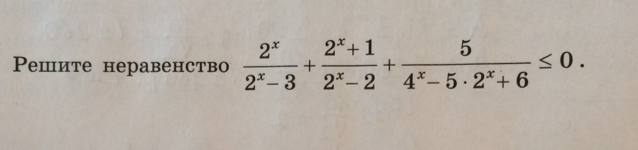
Ответы
Автор ответа:
0
Сделаем замену переменной:
Решаем неравенство:
Последний знаменатель разложим по теореме Виета:
Тогда
Решим неравенство методом интервалов:
0__+__1__+__2__-__3__+__
Нас интересует интервал
Итак,
Переходим обратно к
Ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: RysbekZarina
Предмет: Математика,
автор: peersonee
Предмет: Другие предметы,
автор: bshsshbsbssjs
Предмет: Математика,
автор: Solnyshko1997
Предмет: Алгебра,
автор: nastiaviershin