Предмет: Алгебра,
автор: zodrotik
Найдите угол CDB, если вписанные углы ADB и ADC опираются на дуги окружности, градусные величины которых равны соответственно 128 и 48. Ответ дайте в градусах.
Ответы
Автор ответа:
0
Задача имеет два решения.
I решение
Вписанный угол измеряется половиной дуги, на которую он опирается.
и
Ответ: 40°
II решение.
Ответ: 88°.
Приложения:
Автор ответа:
0
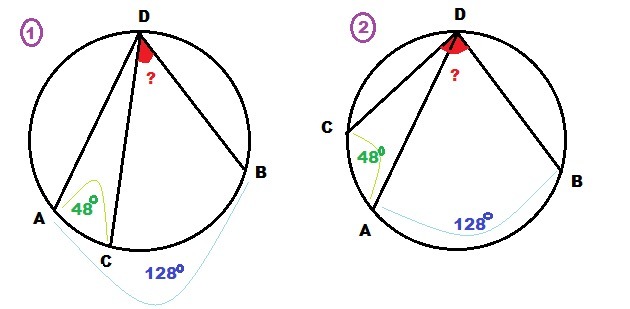
Дуга AB = 128°; дуга AC = 48°. Задача имеет два решения
1) ∪ СВ = ∪ AB - ∪ AC = 128° - 48° = 80°
Величина вписанного угла ∠CDB равна половине градусной меры дуги CB, на которую этот угол опирается.
∠CDB = ∪ CB / 2 = 80° /2 = 40°
∠CDB = 40°
--------------------------------------------------
2) ∪ СВ = ∪ AB + ∪ AC = 128° + 48° = 176°
∠CDB = ∪ CB / 2 = 176° /2 = 88°
∠CDB = 88°
Приложения:
Похожие вопросы
Предмет: Литература,
автор: azizamalik436
Предмет: Химия,
автор: beliksan
Предмет: Химия,
автор: anastasiabebiseva
Предмет: Геометрия,
автор: Sonia1234