Question

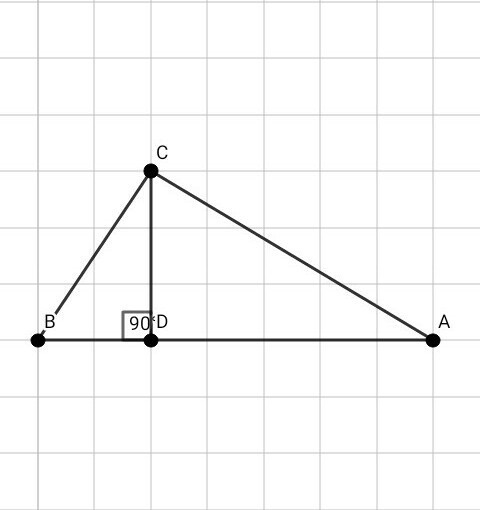
в прямоугольном треугольнике abc угол c=90 градусов,cd высота треугольника,ac= 8 см,cb=6 см.Найдите длину cd

Answer 1

1) Рассмотрим ∆ АВС ( угол С = 90° ):
По теореме Пифагора:
АВ² = ВС² + АС²
АВ² = 8² + 6² = 64 + 36 = 100

Значит, АВ = 10 см

2) Площадь прямоугольного треугольника рассчитывается по формуле через катеты:

S = 1/2 × a × b = 1/2 × BC × AC = 1/2 × 6 × 8 = 24 см²

Но с другой стороны площадь треугольника вычисляется по стороне и высоте, проведенной к этой стороне →

S = 1/2 × AB × CD

24 = 1/2 × 10 × CD

24 = 5 × CD

Значит, CD = 24/5 = 4,8 см

ОТВЕТ: 4,8 см

Answer 2

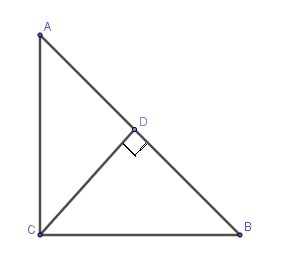
Найдем гипотенузу АВ по теореме Пифагора:

$tt AB^2=AC^2+BC^2\ AB^2=8^2+6^2\ AB^2=100$

$tt AB=10$ см.

Свойства пропорциональных отрезков прямоугольного треугольника

1. Каждый катет есть пропорциональное между гипотенузой и проекцией катета на гипотенузу, то есть

$tt AC^2=ADcdot AB~~~Rightarrow~~~ AD=dfrac{AC^2}{AB}=dfrac{8^2}{10}=6.4~ _{CM}$

Тогда отрезок BD равен: $tt BD=AB-AD=10-6.4=3.6$ см.

2. Высота, опущенная из вершины прямого угла на гипотенузу есть среднее пропорциональное между проекциями катетов, то есть:

$tt CD=sqrt{ADcdot BD}=sqrt{6.4cdot3.6}=sqrt{23.04}=4.8~_{CM}$

Ответ: 4,8 см.