Предмет: Алгебра,
автор: сашаwolwo
1. a) Вычислите площадь фигуры , ограниченной линиями ( сделав рисунок ).
y = 2x²; y=8.
б) Найти - задание во вложении 1.
в) Решить неравенство - задание во вложении 2.
Приложения:
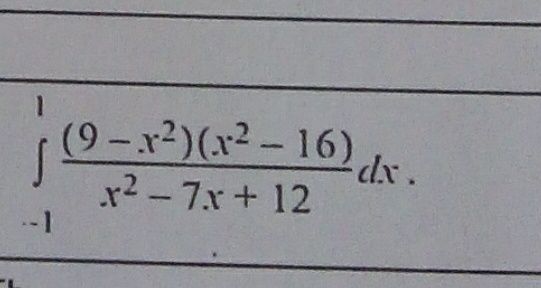

Ответы
Автор ответа:
0
Во первых, максимально упростим подинтегральное выражение:
Если вам не понятно, поясню. В числителе было произведение разностей квадратов, а значит, можно привести данные выражения к более простым (как мы и сделали), а в знаменателе, я разложил многочлен на множители с помощью метода разложения квадратного трехчлена.
Нам осталось решить определенный интеграл через формулу Ньютона-Лейбница:
То есть:
2)
Вначале решим определенный интеграл, а потом неравенство:
Теперь неравенство:
Переносим 9 в лево:
Так как это разность квадратов, получаем:
Есть 2 корня, при котором левое выражение обращается в нуль:
Отметим данные точки на числовой прямой, и получим 3 интервала:
Теперь проверим знаки на каждом из интервалов (нам подойдет интервал со знаком +, так как наше неравенство строго больше нуля).
Отсюда ответ:
3)
Во первых границы фигуры:
График
Понятное дело, что график y=8 выше
Составим определенный интеграл:
По теореме Ньютона-Лейбница, находим:
Похожие вопросы
Предмет: Алгебра,
автор: kurtasmaria59
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: pmp130217
Предмет: Обществознание,
автор: anoni12