Question

Дан четырехугольник MNPK. Известно, что MN||PK, NP||MK. Докажите, что биссектрисы углов N и K параллельны или совпадают




Только напиши в ыоре геометрической задачи, ок?
Типа: дано, решение, пусть , тогда ит.д.

Answer 1

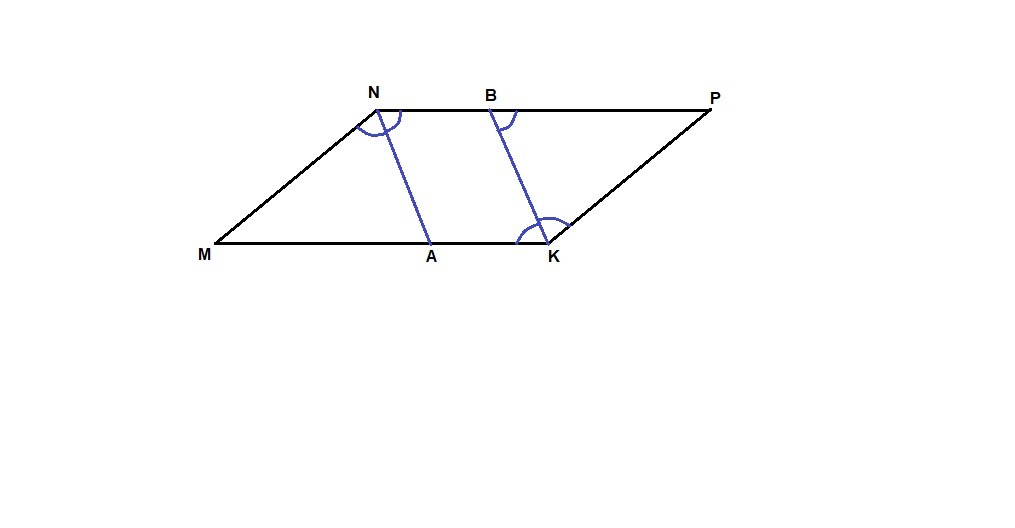
Дано: MNPK - четырехугольник,

          MN║PK, NP║MK,

          NA - биссектриса ∠N,

          KB - биссектриса ∠К.

Доказать: NA║КB или NA и КВ совпадают.

Доказательство:

Так как в четырехугольнике противолежащие стороны параллельны, то это параллелограмм (по определению).

В параллелограмме противолежащие углы равны

∠N = ∠K, значит равны  и их половины:

∠MNA = ∠BNA = ∠РКВ = ∠∠АКВ.

∠РВК = ∠АКВ как накрест лежащие при пересечении параллельных прямых NP и МК секущей КВ, значит

∠РВК = ∠BNA, а эти углы - соответственные при пересечении прямых КВ и NA секущей PN, значит KB║NA.

КВ и NA могут совпадать, если диагональ параллелограмма является биссектрисой углов N и К, т.е. если MNPK ромб.