Предмет: Геометрия,
автор: рюм
ДАЮ 100 БАЛЛОВ ЗА ПОДРОБНОЕ И ПОНЯТНОЕ РЕШЕНИЕ! 4 ЗАДАЧИ! НЕ ЗНАЕШЬ - НЕ ПИШИ, ПОЖАЛУЙСТА! Можно на листике и фото скинуть сюда
Приложения:
Ответы
Автор ответа:
0
Применим теорему синусов : AB: sinC =BC:sin A. Угол А равен 45°.
АВ = ВС * sinC/sinA = 16 * (1/√2) / (√2/2) = 16.
Можно другое объяснение: если синус угла А равен 1/√2, то угол А равен 45° и треугольник является равнобедренным, АВ = ВС = 16.
Если боковая сторона образует с одним основанием угол в 135°, то с другим - угол в 45°, т.к. это односторонние углы при параллельных и секущей.
h = 5 * sin 45° = 5√2/2/
S =(6√2 + 10√2)/2 *(5√2/2) = 8√2 * 5√2/2 = 80/2 = 40.
АВ = ВС * sinC/sinA = 16 * (1/√2) / (√2/2) = 16.
Можно другое объяснение: если синус угла А равен 1/√2, то угол А равен 45° и треугольник является равнобедренным, АВ = ВС = 16.
Если боковая сторона образует с одним основанием угол в 135°, то с другим - угол в 45°, т.к. это односторонние углы при параллельных и секущей.
h = 5 * sin 45° = 5√2/2/
S =(6√2 + 10√2)/2 *(5√2/2) = 8√2 * 5√2/2 = 80/2 = 40.
Автор ответа:
0
Первые задачи решил, а вторые решаются один в один, только числала поменять
Автор ответа:
0
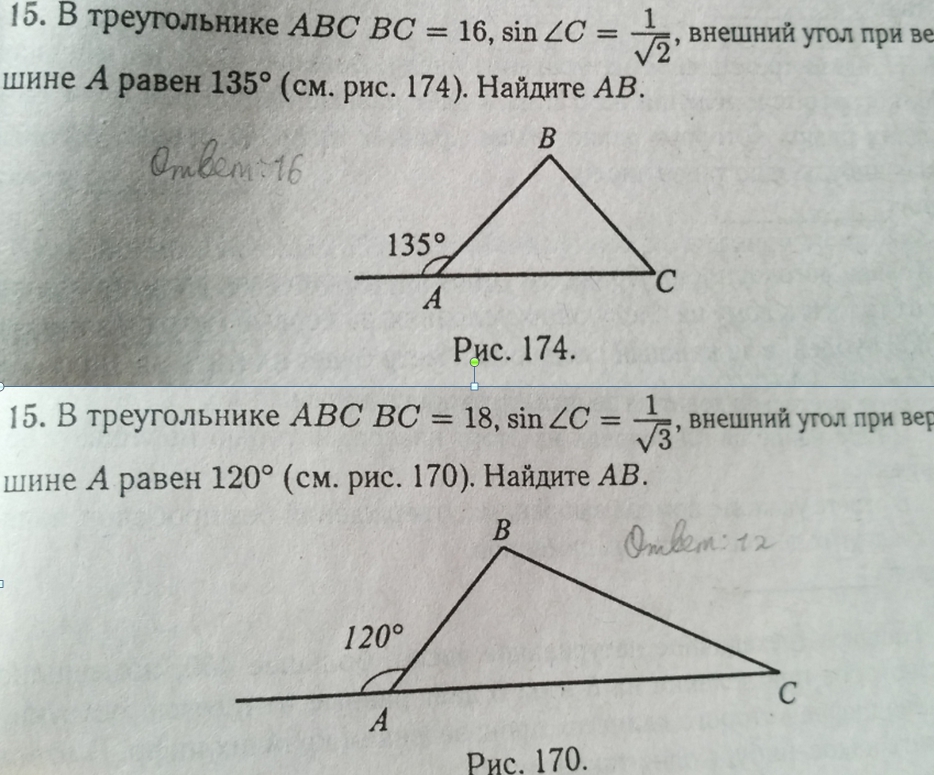
15. рис 174. BC =16 ; sin∠C =1/√2 ; 180° -∠A =135° .
----
AB-?
По теореме синусов : AB/sin∠C=BC/sin∠A ;
∠A =180°-135°=45° ⇒sin∠A=sin45° =1/√2 = sin∠C
следовательно AB =BC=16.
-------
15. рис 170. BC =18 ; sin∠C =1/√3 ; 180° -∠A =120°.
----
AB-?
По теореме синусов : AB/sin∠C=BC/sin∠A ;
∠A =180°-120°=60° ⇒sin∠A=sin60° =√3/2 .
AB/(1/√3) =18/(√3/2)⇔AB√3 =36/√3)⇒AB=36/(√3* √3) =12.
-------
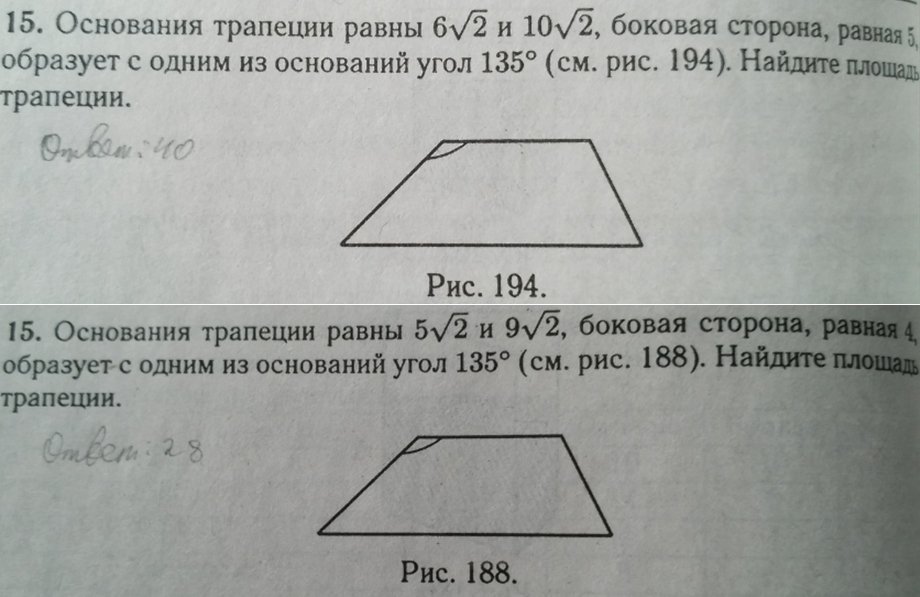
15. рис 194.
AD || BC ; AD =10√2 ; BC =6√2 ; AB =5 ; ∠B =135° .
------
S=S(ABCD) -?
S(ABCD)=(AD+BC)/2 *h =(10√2+6√2)/2 *h = 8√2 *h.
∠A +∠B =180°⇒∠A =180° -135° = 45°.
Из вершины B проведем высоту трапеции BH (опустим перпендикуляр BH⊥AD).Прямоугольный ΔAHB равнобедренный (∠AHB =90° ; ∠A=45°⇒
∠ABH=45°). AH=BH =h . h²+h² =AB² ⇒h =AB/√2 =5/√2 ,следовательно:
S= 8√2 *5/√2 =40.
-------
15. рис 188.
AD || BC ; AD =9√2 ; BC =5√2 ; AB =4 ; ∠B =135° .
------
S=S(ABCD) -?
S(ABCD)=(AD+BC)/2 *h =(9√2+5√2)/2 *h = 7√2 *h.
∠A +∠B =180°⇒∠A =180° -135° = 45°.
Из вершины B проведем высоту трапеции BH (опустим перпендикуляр BH⊥AD).
Из ΔAHB: sin∠A=h/AB⇒h =AB*sin∠A=4*sin45°=4*(1/√2) =4/√2.
следовательно:
S= 7√2 *4/√2 =28.
----
AB-?
По теореме синусов : AB/sin∠C=BC/sin∠A ;
∠A =180°-135°=45° ⇒sin∠A=sin45° =1/√2 = sin∠C
следовательно AB =BC=16.
-------
15. рис 170. BC =18 ; sin∠C =1/√3 ; 180° -∠A =120°.
----
AB-?
По теореме синусов : AB/sin∠C=BC/sin∠A ;
∠A =180°-120°=60° ⇒sin∠A=sin60° =√3/2 .
AB/(1/√3) =18/(√3/2)⇔AB√3 =36/√3)⇒AB=36/(√3* √3) =12.
-------
15. рис 194.
AD || BC ; AD =10√2 ; BC =6√2 ; AB =5 ; ∠B =135° .
------
S=S(ABCD) -?
S(ABCD)=(AD+BC)/2 *h =(10√2+6√2)/2 *h = 8√2 *h.
∠A +∠B =180°⇒∠A =180° -135° = 45°.
Из вершины B проведем высоту трапеции BH (опустим перпендикуляр BH⊥AD).Прямоугольный ΔAHB равнобедренный (∠AHB =90° ; ∠A=45°⇒
∠ABH=45°). AH=BH =h . h²+h² =AB² ⇒h =AB/√2 =5/√2 ,следовательно:
S= 8√2 *5/√2 =40.
-------
15. рис 188.
AD || BC ; AD =9√2 ; BC =5√2 ; AB =4 ; ∠B =135° .
------
S=S(ABCD) -?
S(ABCD)=(AD+BC)/2 *h =(9√2+5√2)/2 *h = 7√2 *h.
∠A +∠B =180°⇒∠A =180° -135° = 45°.
Из вершины B проведем высоту трапеции BH (опустим перпендикуляр BH⊥AD).
Из ΔAHB: sin∠A=h/AB⇒h =AB*sin∠A=4*sin45°=4*(1/√2) =4/√2.
следовательно:
S= 7√2 *4/√2 =28.
Автор ответа:
0
Вот так постарались))) Я долго сижу на этом сайте, но еще никто так подробно не решал) Спасибо огромное!
Автор ответа:
0
Как Вы расставили буквы в задачах с трапецией?
Автор ответа:
0
Начиная с левой вершины нижнего основания по часовой
Автор ответа:
0
A-B-C-D
Автор ответа:
0
Да, спасибо, я понял.
Похожие вопросы
Предмет: Математика,
автор: balmuratova76
Предмет: Информатика,
автор: VladikYm
Предмет: История,
автор: vektop2007
Предмет: Алгебра,
автор: den53mail
Предмет: Обществознание,
автор: vadimnikulin2