Предмет: Алгебра,
автор: Ди14
ПОМОГИТЕ! ОЧЕНЬ СРОЧНО ЛОГАРИФМЫ С РЕШЕНИЕМ
Приложения:

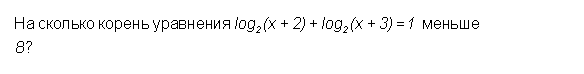
Ответы
Автор ответа:
0
Вспоминая что такое логарифм, получаем:
Теперь раскроем модуль:
Получаем:
Данный корень, подходит к 1 условию в системе неравенств.
Теперь 2 случай, когда это выражение меньше нуля:
Данный корень подходит к 2 условию в системе, но мы знаем что выражение в логарифме, всегда положительно. Поэтому 2 корень не подходит.
Получаем 1 корень:
2)
По свойству логарифма, объединяем данные логарифмы:
Раскроем скобки:
Теперь, по свойству логарифма, получаем:
Переносим все в право, и получаем:
корни:
Теперь проверим, какие корни совпадают с условием логарифма:
В логарифмах получается положительное число, поэтому этот корень подходит.
Сделаем ту же операцию и с 2 корнем, получим, отрицательные числа. А значит, он не подходит.
Получаем 1 корень:
На сколько он меньше 8:
На 7.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: churka2506
Предмет: Биология,
автор: Roma666666666
Предмет: Физика,
автор: Kulzen
Предмет: География,
автор: glimba200