Предмет: Математика,
автор: basovvova96
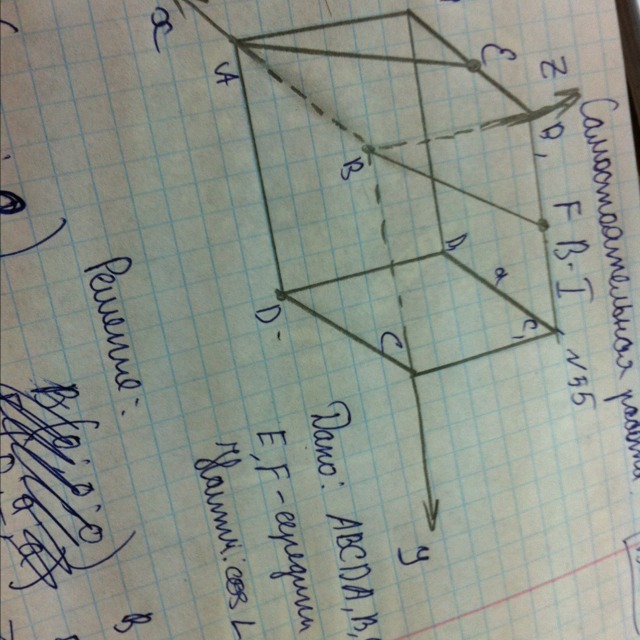
В кубе абсда1б1с1д1 точки Е и ф середины ребер соответственно а1б1 и б1с1. Найдите косинус между прямыми ае и бф
Приложения:
Ответы
Автор ответа:
0
Идеология предыдущего решения верна, но неверно само решение ;)
Координаты точек в выбранной системе координат
A(2,0,0)
B(0,0,0)
E(1,0,2)
F(0,1,2)
Тогда координаты векторов
AE = (1,0,2) - (2,0,0) = (-1,0,2)
BF = (0,1,2) - (0,0,0) = (0,1,2)
Скалярное произведение векторов равно
AE x BF = (-1,0,2) x (0,1,2) = (-1*1 + 0*1 + 2*2) = -1 + 4 = 3
Модули векторов
|AE| = sqrt(1+0+4) = sqrt(5)
|BF| = sqrt(0+1+4) = sqrt(5)
cos A = (AE x BF) / (|AE|*|BF|) = 3 / 5 = 0.6
Похожие вопросы
Предмет: Русский язык,
автор: arsenlike
Предмет: Русский язык,
автор: aardak815
Предмет: История,
автор: ositc
Предмет: Математика,
автор: tg12122002