Предмет: Алгебра,
автор: manaka13
решите, пожалуйста.
номер #156.
Приложения:
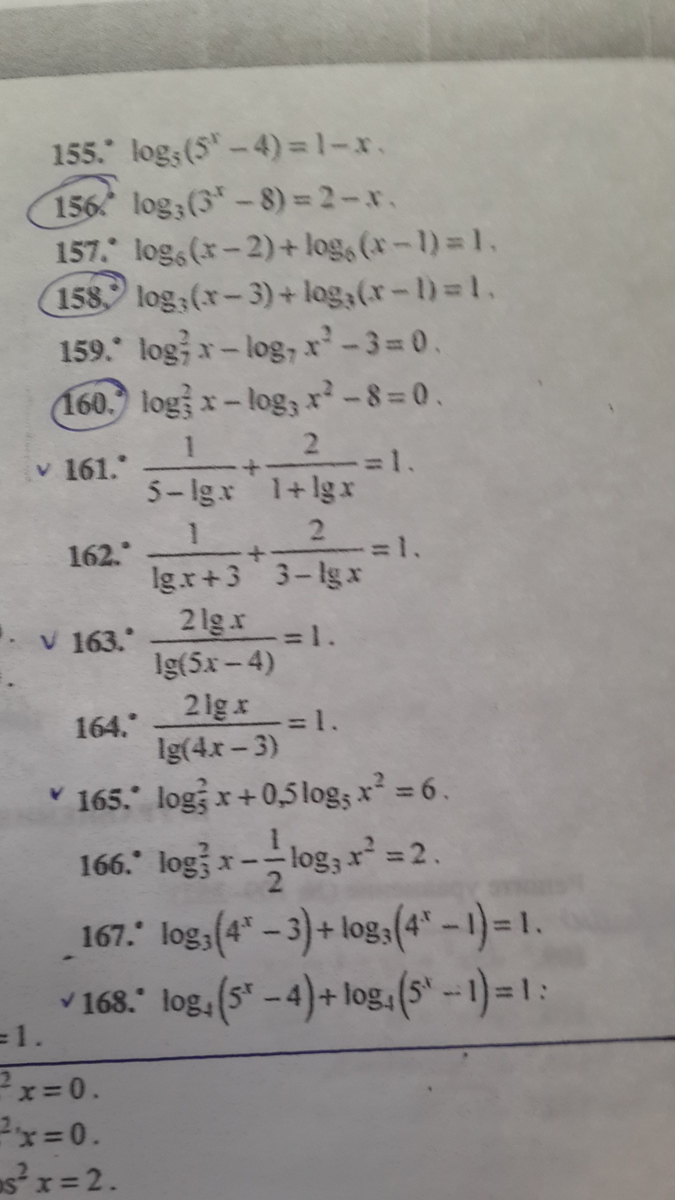
Ответы
Автор ответа:
0
По определению логарифма:
3^2-х=(3^х)-8
Если в степени разность, значит, это деление, т.е.:
3^2/3^х=(3^х)-8
Сделаем замену, пусть 3^х=у, тогда:
9/у=у-8
у(у-8)=9
у^2-8у-9=0
Д=64-4*(-9)=100
у1=8-10/2=-1
у2=8+10/2=9
Возвращаемся к замене:
3^х=9
х=2
3^х=-1, решений нет, т.к. 3^х>0 всегда (это показательная функция)
3^2-х=(3^х)-8
Если в степени разность, значит, это деление, т.е.:
3^2/3^х=(3^х)-8
Сделаем замену, пусть 3^х=у, тогда:
9/у=у-8
у(у-8)=9
у^2-8у-9=0
Д=64-4*(-9)=100
у1=8-10/2=-1
у2=8+10/2=9
Возвращаемся к замене:
3^х=9
х=2
3^х=-1, решений нет, т.к. 3^х>0 всегда (это показательная функция)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Musa1net
Предмет: Математика,
автор: yanabalchenkova
Предмет: Математика,
автор: bpass508
Предмет: Физика,
автор: Nadia715
Предмет: Математика,
автор: даша85469231025