Предмет: Алгебра,
автор: devi321
Помогите!!! Покажите как решить (подробно)
Приложения:
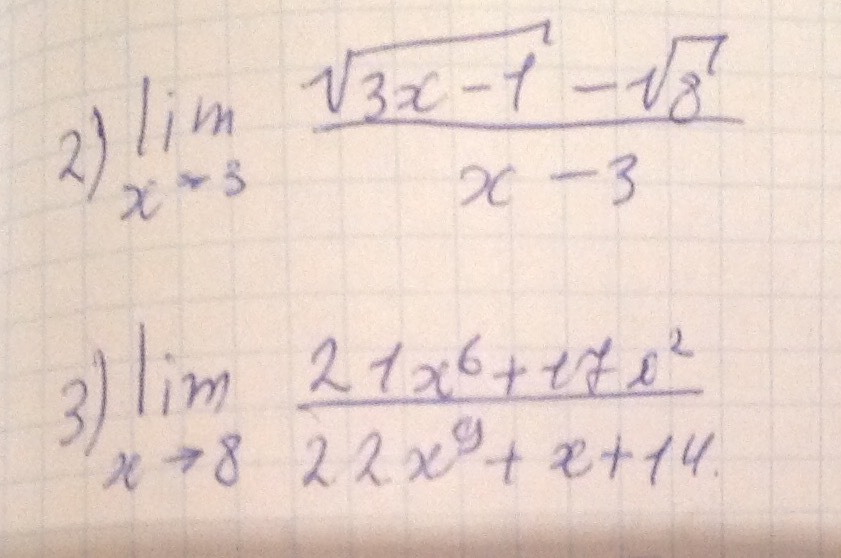
Ответы
Автор ответа:
0
2) 
подставляем вместо х 3. получаем неопределенность 0/0
тогда домножаем и числитель и знаменатель на сопряженное числителю выражение
 =
=
=
3)
А если это было не 8 а ∞ то

подставляем вместо х 3. получаем неопределенность 0/0
тогда домножаем и числитель и знаменатель на сопряженное числителю выражение
=
3)
А если это было не 8 а ∞ то
Похожие вопросы
Предмет: Другие предметы,
автор: ertajzanerke43
Предмет: История,
автор: Аноним
Предмет: Физкультура и спорт,
автор: sofisot13
Предмет: Химия,
автор: lapusic98
Предмет: Математика,
автор: Рафаэль123