Question

Задание во вложении! .....................

Answer 1

1)
$y=x^2-5x+6$
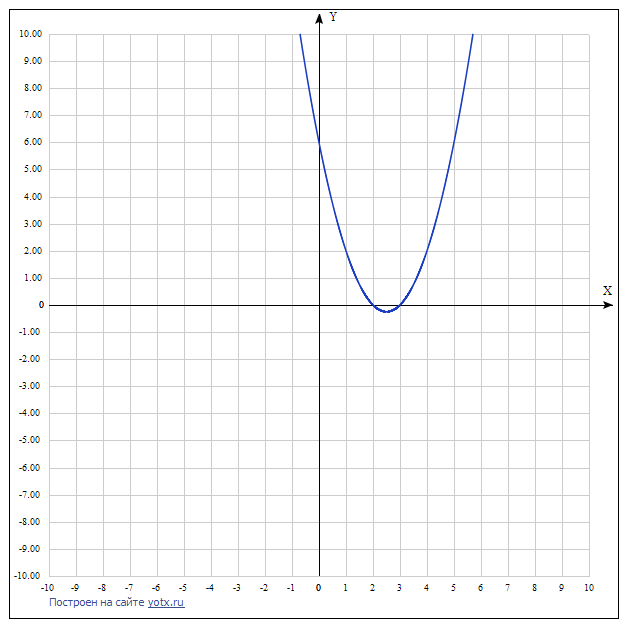
Так как это квадратная функция, ее график, парабола.
В данной функции, коэффициент $a$ перед иксом положителен и равен 1, поэтому ветви параболы направлены вверх.
Найдем вершину параболы (m,n):
$m= frac{-b}{2a}= frac{5}{2}= 2 frac{1}{2}$
$n= -frac{b^2-4ac}{4a} = -frac{25-24}{4}= - frac{1}{4}$
Область определения:
$D(f)= mathbb R$
Область значений:
$E(f)= (- frac{1}{4}, +infty )$
Уравнение оси симметрии :
$x= 2 frac{1}{2}$

Теперь подставляем значения икса по этим условиям и получаем график (во вложении).

2)
Подставляем вместо икса данное значение:
$y=1,5^2-5*1,5+6$
$y= 2,5-7,5+6=1$

3) 
Подставляем вместо игрека 5:
$5=x^2-5x+6$
$x^2-5x+1=0$
$D= sqrt{b^2-4ac}= sqrt{25-4}= sqrt{21}$
$x_{1,2}= frac{5pm sqrt{21} }{2}$

4)
Надо найти $f(x)=0$
Получаем:
$x^2-5x+6=0$
$D= sqrt{b^2-4ac}= sqrt{25-24}= 1$
$x_{1,2}= frac{5pm1}{2} = 3,2$ - это не дробь , это 2 корня.

Теперь запишем интервалы, на которых меняется знак значения функции:
f(x)>0 на интервале 
$(-infty,2)cup(3,+infty)$
f(x)<0 на интервале:
$(2,3)$

5)
Теперь самое сложное :)

Найдем производную данной функции:
$f(x)=x^2-5x+6$
$f'(x)= 2x-5$
Находим область определения производной.
$D(f)= mathbb R$
Решаем теперь уравнение:
$2x-5=0$
$x=2 frac{1}{2}$
Отмечаем эту точку на числовой прямой.
Имеем 2 интервала:
$(-infty , 2 frac{1}{2})(2 frac{1}{2}+infty)$
Находим знаки на каждой из интервалов, получаем что на интервале:
$(-infty , 2 frac{1}{2})$ значение производной отрицательно.
на интервале $(2 frac{1}{2}+infty)$ значение производной положительно.
Получаем:
Функция убывает на интервале:
$(-infty , 2 frac{1}{2})$
Функция возрастает на интервале:
$(2 frac{1}{2}, +infty )$

6)
Ну при построении графика мы уже нашли эту область :)
$E(f)= (- frac{1}{4}, +infty )$