Предмет: Алгебра,
автор: ameliqwerty
решите задание с параметром
НЕ графически
Приложения:
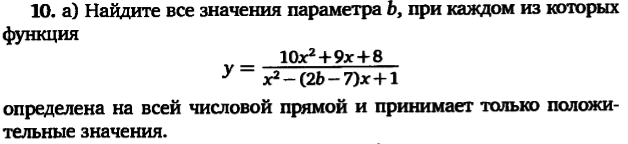
Ответы
Автор ответа:
0
дробь a/b>0, если числитель и знаменатель одинаковых знаков(оба положительны или оба отрицательны).
y=(10x²+9x+8)/(x²-(2b-7)x+1))
числитель: 10x²+9x+8>0 при любых значениях х.
D=9²-4*10*8=81-320<0
знаменатель (x²-(2b-7)x+1)>0, если D<0
D=(2b-7)²-4*1*1
(2b-7)²-4<0
(2b-7)²-2²<0
(2b-7-2)*(2b-7+2)<0
(2b-9)*(2b-5)<0
2,5<b<4,5
ответ: при 2,5<b<4,5 функция принимает положительные значения на всей числовой прямой
y=(10x²+9x+8)/(x²-(2b-7)x+1))
числитель: 10x²+9x+8>0 при любых значениях х.
D=9²-4*10*8=81-320<0
знаменатель (x²-(2b-7)x+1)>0, если D<0
D=(2b-7)²-4*1*1
(2b-7)²-4<0
(2b-7)²-2²<0
(2b-7-2)*(2b-7+2)<0
(2b-9)*(2b-5)<0
2,5<b<4,5
ответ: при 2,5<b<4,5 функция принимает положительные значения на всей числовой прямой
Автор ответа:
0
Ответ не сходится, должно было получитья (2,5;4,5). Но все равно спасибо!!
Автор ответа:
0
спасибо. я нашла свою ошибку. разность квадратов неправильно применила.
(2b-7)^2-2^2=(2b-7-2)*(2b-7+2)=(2b-9)*(2b-5). =>
2,5<b<4,5
(2b-7)^2-2^2=(2b-7-2)*(2b-7+2)=(2b-9)*(2b-5). =>
2,5<b<4,5
Автор ответа:
0
Спасибо!
Похожие вопросы
Предмет: Французский язык,
автор: Аноним
Предмет: Английский язык,
автор: cuteboy13095
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Лайвир