Question

Расстояния от точки пересечения медиан равнобедренного треугольника до сторон равны 8 см,8 см и 5 см.Найдите стороны треугольника

Answer 1

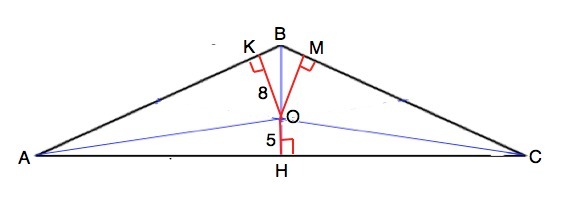
Обозначим данный треугольник АВС, ВН медиана к основанию, О - точка пересечения медиан.
ОК=ОМ=8, ОН=5.
Медианы треугольника пересекаются в одной точке, которая делит их в отношении 2:1, считая от вершины. ⇒
ОВ=2ОН=10 см.
Медиана ВН=ОН+ОВ=15 см. 
Для равнобедренного треугольника медиана, проведенная к основанию,  еще биссектриса и высота. ⇒
∆ ВНС - прямоугольный. 
Расстояние от точки до прямой равно длине проведенного к ней перпендикуляра. ⇒
∆ ВОМ = ∆ ВОК - прямоугольные с гипотенузой ВО=10
По т.Пифагора или обратив внимание на отношение катета и гипотенузы ( египетский треугольник), найдём длину ВК=ВМ=6 см. 
В прямоугольных треугольниках ВОМ и ВСН угол В - общий. ⇒
Эти треугольники подобны по равному острому углу. 
Из подобия следует отношение: 
ВО:ВС=ВМ:ВН
 10:ВС=6:15 ⇒
ВС=25 см.
Медианы треугольника делят его на равновеликие треугольники. 
S ∆ АОС=S ∆ BOC =S ∆ BOA⇒
ОМ•ВС=ОН•АС
8•25=5•АС⇒
АС=40 см
Стороны данного треугольника АВ=СВ=25 см, АС=40 см. 

Answer 2

Точка О - пересечение медиан, делит каждую медиану в отношении 2:1, считая от вершины (свойство). Значит ВО=10, а ВН=15.
Проведем перпендикуляр ОК - расстояние от точки О до прямой ВС.
Из прямоугольного треугольника ВОК по Пифагору ВК=√(10²-8²)= 6см.  КС=ВС-ВК=ВС-6.
Из прямоугольного треугольника КОС по Пифагору ОС²=ОК²+КС².
ОС²= 8²+(ВС-6)² = 64+ВС²-12ВС+36 =ВС²-12ВС+100 (1).
В равнобедренном треугольнике ВН - медиана и высота.
Из прямоугольного треугольника НОС по Пифагору
ОС²=ОН²+НС² = 25+НС². 
Из прямоугольного треугольника ВНС по Пифагору НС²=ВС²-15².
Тогда ОС²=25+ВС²-225 = ВС²-200  (2).
Приравняем (1) и (2):
ВС²-12ВС+100=ВС²-200  =>  12ВС=300  и  ВС=25. АВ=ВС=25см.
НС²=ВС²-15²=НС²=25²-15²=400 и
АС=2*НС = 40см.
Ответ: стороны треугольника равны 25,25 и 40.