Question

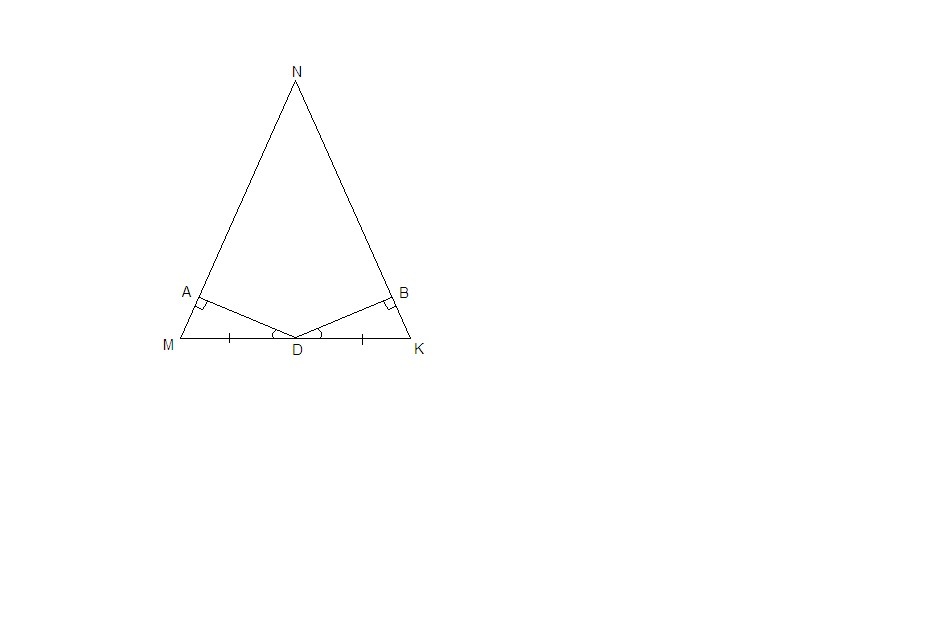
В остроугольном треугольнике MNK из точки  D - середины стороны MK - проведены перпендикуляры DA и DB к сторонам MN и NK. Докажите, что если угол ADM=углу BDK то треугольник MNK равнобедренный

Answer 1

∠DAM = ∠DBK = 90°,
∠ADM = ∠BDK по условию,
MD = DK по условию, ⇒
ΔDAM = ΔDBK по гипотенузе и острому углу.
Из равенства треугольников следует, что
∠AMD = ∠BKD, т.е. что в ΔMNK равны два угла. А если в треугольнике равны два угла, то он равнобедренный (признак равнобедренного треугольника).
Значит, ΔMNK равнобедренный.