Question

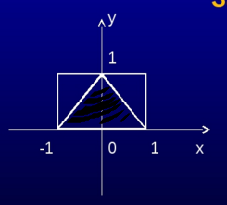
Определить методом Монте-Карло площадь треугольника, вершины которого имеют координаты (-1,0) ; (0,1) ; (1,0)
Подсказка : треугольник заключен в прямоугольник со сторонами а=1 и b=2
Нужно в Паскале это сделать!!!
Помогите, пожалуйста...
И еще , учительница сказала , что вроде как надо модуль использовать...

Answer 1

Условие попадания точки M(x,y) в треугольник с указанными координатами вершин можно описать системой неравенств:
$displaystyle left{begin{matrix} ygeqslant 0 \ yleqslant x+1 \ yleqslant 1-x end{matrix}right$

Если положить в методе Монте-Карло x∈(-1,1), y∉(0,1) для вещественных х,y,
то площадь треугольника можно найти, как площадь прямоугольника, представленного в задании (она равна 2), умноженную на отношение количества точек, попавших в контур треугольника, к общему количеству точек.

// PascalABC.NET 3.0, сборка 1160 от 05.02.2016
begin
  var n:=100000;
  var k:=Range(1,n).Select(e->Rec(2*Random()-1,Random())).
    Where(e->(e.Item2>=0) and (e.Item2<=e.Item1+1) and
    (e.Item2<=1-e.Item1)).Count;
  Writeln(2*k/n:0:3)
end.

Тестовое решение:
1.001

Answer 2

Если кому-то нужно с ABS, можно так написать определение k:
var k:=Range(1,n).Select(e->Rec(2*Random()-1,Random())).
Where(e->(e.Item2>=0) and (e.Item2<=1-abs(e.Item1))).Count;