Предмет: Геометрия,
автор: vladalopatina
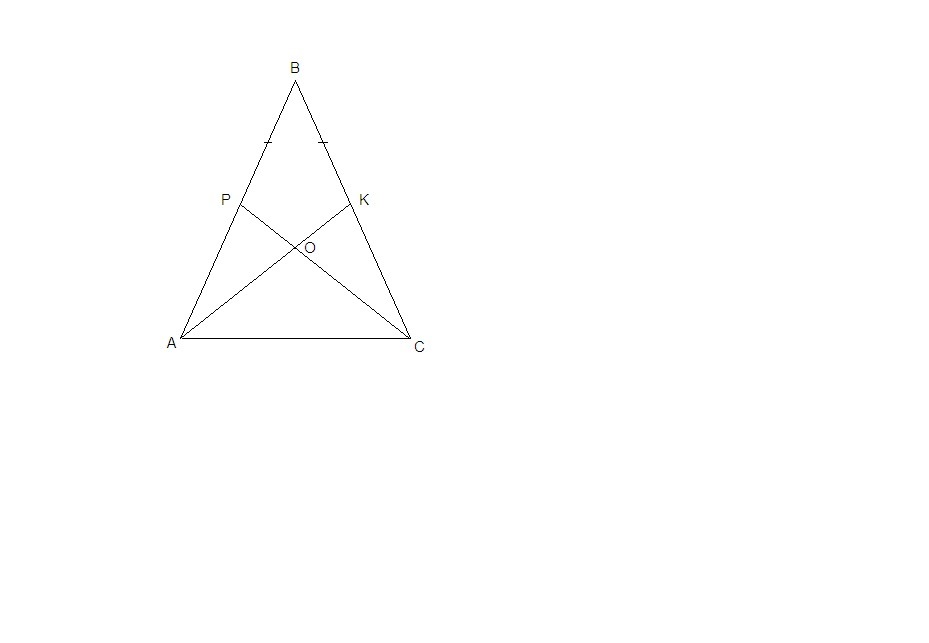
Треугольник ABC равнобедренный с основанием AC. На сторонах AB и BC отмечены точки P и K так, что BP=BK. O- точка пересечения AK и CP. Докажите что треугольник AOC равнобедренный
Ответы
Автор ответа:
0
ВР = ВК по условию,
ВС = ВА по условию,
∠В - общий для треугольников ВАК и ВСР, ⇒
ΔВАК = ΔВСР по двум сторонам и углу между ними.
Значит, ∠ВАК = ∠ВСР.
∠ОАС = ∠ВАС - ∠ВАК
∠ОСА = ∠ВСА - ∠ВСР,
Углы ВАС и ВСА равны как углы при основании равнобедренного треугольника, значит
∠ОАС = ∠ОСА и следовательно
ΔОАС - равнобедренный.
ВС = ВА по условию,
∠В - общий для треугольников ВАК и ВСР, ⇒
ΔВАК = ΔВСР по двум сторонам и углу между ними.
Значит, ∠ВАК = ∠ВСР.
∠ОАС = ∠ВАС - ∠ВАК
∠ОСА = ∠ВСА - ∠ВСР,
Углы ВАС и ВСА равны как углы при основании равнобедренного треугольника, значит
∠ОАС = ∠ОСА и следовательно
ΔОАС - равнобедренный.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: polinka4614
Предмет: Физика,
автор: fghuuyg
Предмет: Физика,
автор: просто1000000
Предмет: Математика,
автор: makoveenko2015