Question

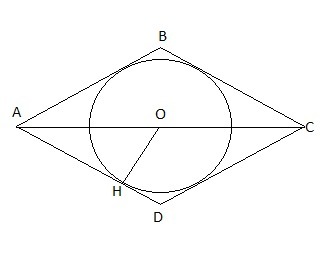
Большая диагональ ромба равна 24, а один из углов 60. Найти длину вписанной окружности

Answer 1

Центр вписанной в ромб окружности находится в точке пересечения его диагоналей, которая делит их пополам.

AO = AC / 2 = 24 / 2 = 12

Диагональ AC является биссектрисой ∠BAD ⇒

∠OAD = ∠BAD / 2 = 60° / 2 = 30°

В прямоугольном ΔAOH против угла в 30° лежит половина гипотенузы:

OH = AO / 2 = 12 / 2 = 6

Зная радиус вписанной окружности r = OH найдем длину вписанной окружности:

C = 2 * π * r = 2 * π * 6 = 12π

Ответ: длина вписанной окружности равна 12π