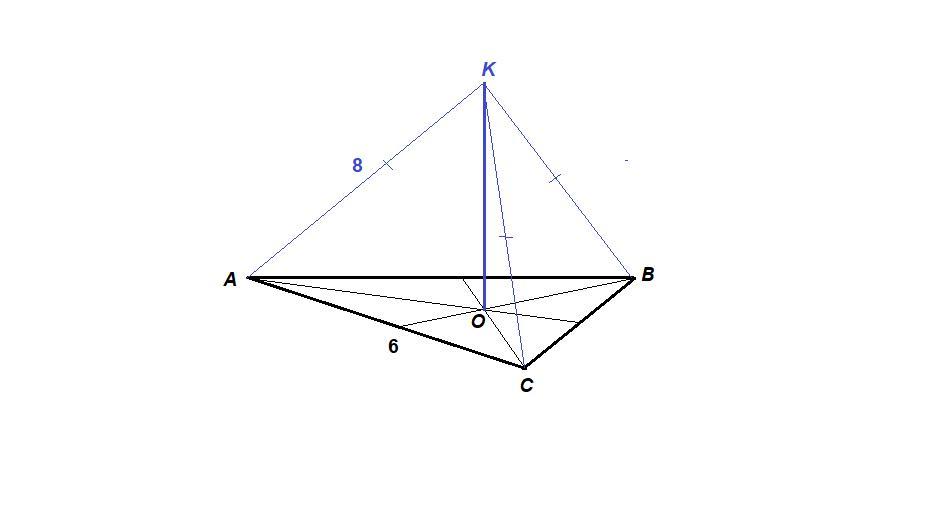
найти расстояние от точки К до плоскости равностороннего треугольника со стороной 6 см и равноуд. от его вершин на расстояние 8 см
Ответы
1) Т. к. в основании пирамиды лежит правильный треугольник (назовем его АВС), то расстояние от К до его плоскости есть высота пирамиды и она проецируется в центр основания, т.е. в точку О пересечения высот(медиан и биссектрис) правильного треугольника.
2) Высота основания ВВ1 = √(6²+3²) = √27 = 3√3
3) Центр основания делит высоты в правильном треугольнике в отношении 2:1, считая от вершины В. Т. Е. ВО:В1О = 2:1 ⇒ ВО = 2√3
4) по теореме Пифагора КО² = КВ² - ВО² = 8² - (2√3)² = 64 - 12 = 52 ⇒ КО = √52 = 2√13
Ответ: 2√13
Ответ: 2√13 см
Объяснение:
КО - перпендикуляр к плоскости равностороннего треугольника АВС.
КО - искомое расстояние.
Так как КО перпендикуляр к плоскости, то отрезок КО перпендикулярен любой прямой плоскости.
∠КОА = ∠КОВ = ∠КОС = 90°,
КА = КВ = КС = 8 см по условию,
КО - общий катет для треугольников КОА, КОВ и КОС, ⇒
ΔКОА = ΔКОВ = ΔКОС по катету и гипотенузе. значит
ОА = ОВ = ОС, тогда О - центр правильного треугольника АВС.
ОА = АВ√3/3 как радиус окружности, описанной около равностороннего треугольника,
ОА = 6√3/3 = 2√3 см
ΔKOA: ∠KOA = 90°, по теореме Пифагора
KO = √(KA² - OA²) = √(8² - (2√3)²) = √(64 - 12) = √52 = 2√13 см