Question

По­строй­те гра­фик функ­ции y=(x-9)(x^2-9)/(x^2-6x-27) и опре­де­ли­те, при каких зна­че­ни­ях по­стро­ен­ный гра­фик не будет иметь общих точек с пря­мой y=kx

Answer 1

Область определения функции: функция существует, если знаменатель дроби не обращается в нуль, т.е. $tt x^2-6x-27ne 0$

$tt (x-3)^2-36ne 0\ (x-3-6)(x-3+6)ne 0\ (x-9)(x+3)ne 0\ x_1ne 9\ x_2ne -3$

Упростим функцию: $tt displaystyle y=frac{(x-9)(x-3)(x+3)}{(x+3)(x-9)}=x-3$

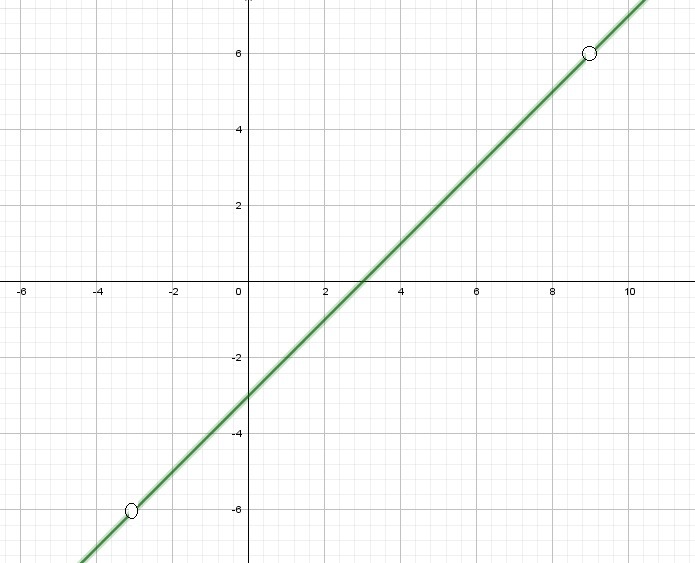
Получили линейную функцию; графиком линейной функции является прямая, проходящая через точки (0;-3), (3;0).

Графики функций не имеют общих точек, если $tt y=kx$ проходит через выколотые точки, т.е. через точки $tt (9;6),~ (-3;-6)$

Подставляя координаты, получим:

$tt 6=9k ~~~Rightarrow~~~ boxed{tt k=frac{2}{3}} \ \ -6=-3k~~~Rightarrow~~~ boxed{tt k=2}$

Решим теперь уравнение $tt kx=x-3~~Rightarrow~~ x=dfrac{3}{1-k}$

Очевидно, что при $tt boxed{tt k=1}$ уравнение решений не имеет, а следовательно, графики функций при k=1 не имеют общих точек.

Ответ: 2/3; 1; 2.