Предмет: Геометрия,
автор: ertyuiop123
ПОМОГИТЕ ОТВЕТИТЬ НА 5 ВОПРОСОВ!
1. Чему равна высота правильной треугольной пирамиды со стороной основания а и боковым ребром b?
2. Чему равна сторона основания правильной шестиугольной пирамиды, если её высота h и боковое ребро b?
3. Чему равна высота правильной шестиугольной пирамиды со стороной основания а и боковым ребром b?
4. Чему равна апофема правильной четырехугольной пирамиды со стороной основания а и высотой h?
5. Чему равна апофема правильной треугольной пирамиды со стороной а и боковым ребром b?
Ответы
Автор ответа:
0
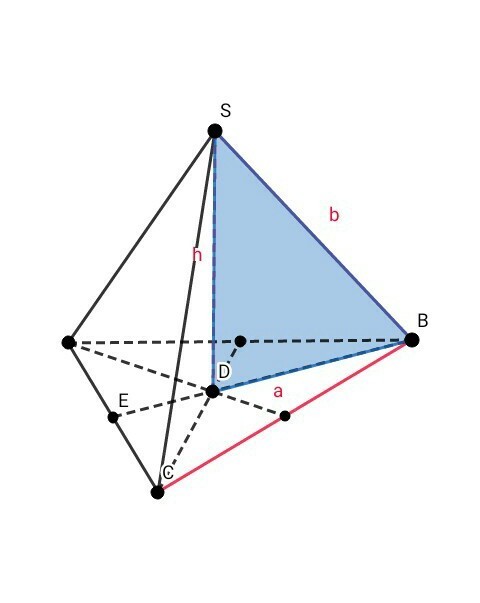
1) см. рис. 1 :
В основании правильной треугольной пирамиды лежит равносторонний треугольник
Высота равностороннего треугольника вычисляется по формуле:

где а - сторона равностороннего треугольника
Вершина пирамиды проецируется в центр основания. Центром равностороннего треугольника является точка пересечения биссектрис, медиан и высот.
Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 : 1 , считая от вершины →
BD = ( a√3 / 2 ) × 2/3 = a√3 / 3
Рассмотрим ∆ SBD (угол SDB = 90°):
По теореме Пифагора:
SB² = SD² + BD²
h² = b² - ( a√3 / 3 )²

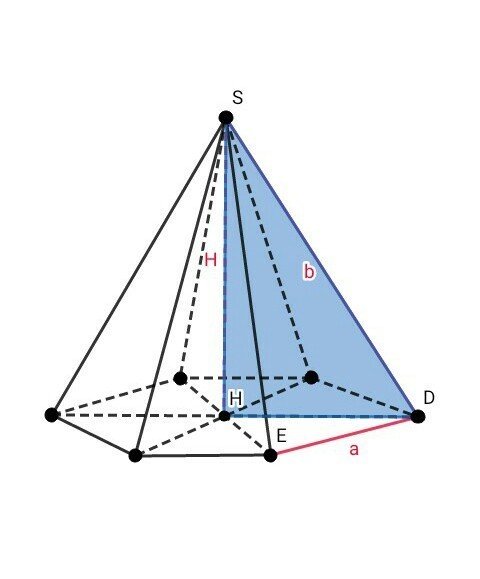
2) см. рис. 2:
В основании правильной шестиугольной пирамиды лежит правильный шестиугольник
Бо'льшие диагонали правильного шестиугольника пересекаются в одной точке и точкой пересечения делятся пополам, и при этом эти диагонали делят шестиугольник на шесть равных равносторонних треугольников →
HD = DE = a - сторона основания
Рассмотрим ∆ SDH (угол SHD = 90°):
По теореме Пифагора:
SD² = SH² + HD²
a² = b² - h²

3) см. рис. 2 :
Рассмотрим ∆ SDH (угол SHD = 90°):
По теореме Пифагора:
SD² = SH² + HD²
h² = b² - a²

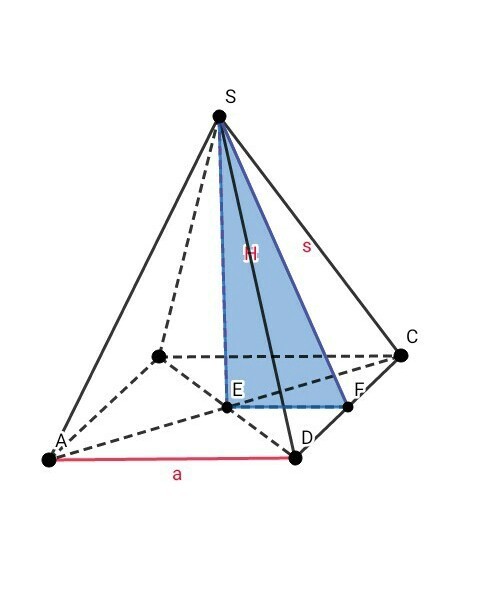
4) см. рис. 3 :
В основании правильной четырёхугольной пирамиды лежит квадрат
Опустим из точки Е – точки пересечения диагоналей квадрата – перпендикуляр EF к CD →
По теореме о трёх перпендикулярах получаем, что SF перпендикулярен CD, то есть SF = s – апофема пирамиды
Рассмотрим ∆ CDE (угол CED = 90°):
∆ CDE – прямоугольный и равнобедренный, так как диагонали квадрата равны и точкой пересечения делятся пополам →
EF – высота, медиана, биссектриса
Поэтому, EF = a / 2
Рассмотрим ∆ SEF (угол SEF = 90°):
По теореме Пифагора:
SF² = SE² + EF²
s² = h² + ( a / 2 )²

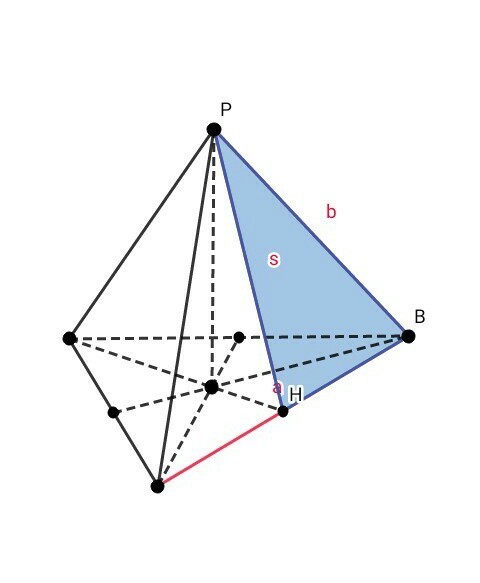
5) см. рис. 4 :
РН = s — апофема пирамиды
Так как все боковые ребра правильной треугольной пирамиды равны →
РН – высота, медиана, биссектриса боковой грани. Поэтому ВН = а / 2
Рассмотрим ∆ BPH (угол PHB = 90°):
По теореме Пифагора:
РВ² = PH² + BH²
s² = b² - ( a/2 )²

В основании правильной треугольной пирамиды лежит равносторонний треугольник
Высота равностороннего треугольника вычисляется по формуле:
где а - сторона равностороннего треугольника
Вершина пирамиды проецируется в центр основания. Центром равностороннего треугольника является точка пересечения биссектрис, медиан и высот.
Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 : 1 , считая от вершины →
BD = ( a√3 / 2 ) × 2/3 = a√3 / 3
Рассмотрим ∆ SBD (угол SDB = 90°):
По теореме Пифагора:
SB² = SD² + BD²
h² = b² - ( a√3 / 3 )²
2) см. рис. 2:
В основании правильной шестиугольной пирамиды лежит правильный шестиугольник
Бо'льшие диагонали правильного шестиугольника пересекаются в одной точке и точкой пересечения делятся пополам, и при этом эти диагонали делят шестиугольник на шесть равных равносторонних треугольников →
HD = DE = a - сторона основания
Рассмотрим ∆ SDH (угол SHD = 90°):
По теореме Пифагора:
SD² = SH² + HD²
a² = b² - h²
3) см. рис. 2 :
Рассмотрим ∆ SDH (угол SHD = 90°):
По теореме Пифагора:
SD² = SH² + HD²
h² = b² - a²
4) см. рис. 3 :
В основании правильной четырёхугольной пирамиды лежит квадрат
Опустим из точки Е – точки пересечения диагоналей квадрата – перпендикуляр EF к CD →
По теореме о трёх перпендикулярах получаем, что SF перпендикулярен CD, то есть SF = s – апофема пирамиды
Рассмотрим ∆ CDE (угол CED = 90°):
∆ CDE – прямоугольный и равнобедренный, так как диагонали квадрата равны и точкой пересечения делятся пополам →
EF – высота, медиана, биссектриса
Поэтому, EF = a / 2
Рассмотрим ∆ SEF (угол SEF = 90°):
По теореме Пифагора:
SF² = SE² + EF²
s² = h² + ( a / 2 )²
5) см. рис. 4 :
РН = s — апофема пирамиды
Так как все боковые ребра правильной треугольной пирамиды равны →
РН – высота, медиана, биссектриса боковой грани. Поэтому ВН = а / 2
Рассмотрим ∆ BPH (угол PHB = 90°):
По теореме Пифагора:
РВ² = PH² + BH²
s² = b² - ( a/2 )²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: krimsveta40
Предмет: Математика,
автор: kiksarinameruert38
Предмет: Геометрия,
автор: furman07
Предмет: Химия,
автор: Valer4ik232