Пожалуйста помогите решить!!!Даю много баллов!!!!
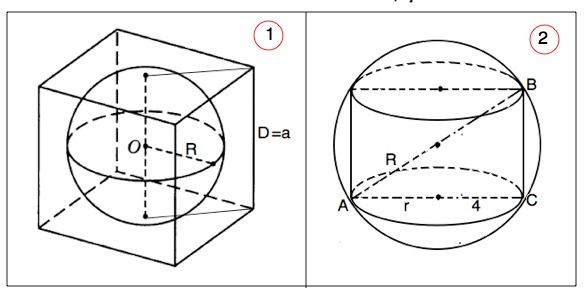
1. В куб вписан шар. Найдите площадь поверхности шара, если площадь полной поверхности куба равна 1170/π.
2. В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найдите высоту цилиндра, если радиус его основания равен 4.
Если можно, то распишите как можно подробнее. Буду очень признательна и отмечу ответ как лучший. Действительно очень важно!!!
Ответы
1)
Диаметр вписанного в куб шара равен длине ребра куба, а радиус - половине длины ребра.
Площадь полной поверхности куба равна сумме площадей его 6-ти граней.
Площадь одной грани равна а² =1170/π :6=195/π
R²= (a/2)²=195/4π
Из формулы площади поверхности шара
S=4πR²=4π•195/4π=195 (ед. площади)
2)
Окружности, ограничивающие основания вписанного цилиндра изнутри касаются шара.
Осевое сечение цилиндра - прямоугольник, проходит через центр шара, при этом диаметр шара является диагональю этого прямоугольника.
Из формулы площади поверхности сферы 4πR²=100π находим её радиус R=5 ⇒ D=10
Диаметр основания цилиндра d=2r=8.
Из прямоугольного ∆ АВС высота ( образующая) цилинда ВС=6 ( по т.Пифагора или обратив внимание на отношение катета АС и гипотенузы АВ 4:5 - отношение сторон "египетского" треугольника)
Высота цилиндра - 6 ед. длины.