Предмет: Алгебра,
автор: ruslandio123
sin^2(1/2 arcsin3/7) - cos^2(1/2 arcsin3/7) - Вычислите
Ответы
Автор ответа:
0
Для краткости сделаю замену 1/2 arcsin3/7=t
sin^2(t) - cos^2(t)=-cos(2t), вернем arcи
cos(arcsin3/7). вообще, дальше я хз как, но инет говорит, что cos(arcsinx)=sqrt(1-x^2), т.е. получим
cos(acrsin3/7)=sqrt(1-9/49)= sqrt(40)/7= 2sqrt(10)/7, вероятнее всего, ответ должен быть такой.
sin^2(t) - cos^2(t)=-cos(2t), вернем arcи
cos(arcsin3/7). вообще, дальше я хз как, но инет говорит, что cos(arcsinx)=sqrt(1-x^2), т.е. получим
cos(acrsin3/7)=sqrt(1-9/49)= sqrt(40)/7= 2sqrt(10)/7, вероятнее всего, ответ должен быть такой.
Приложения:
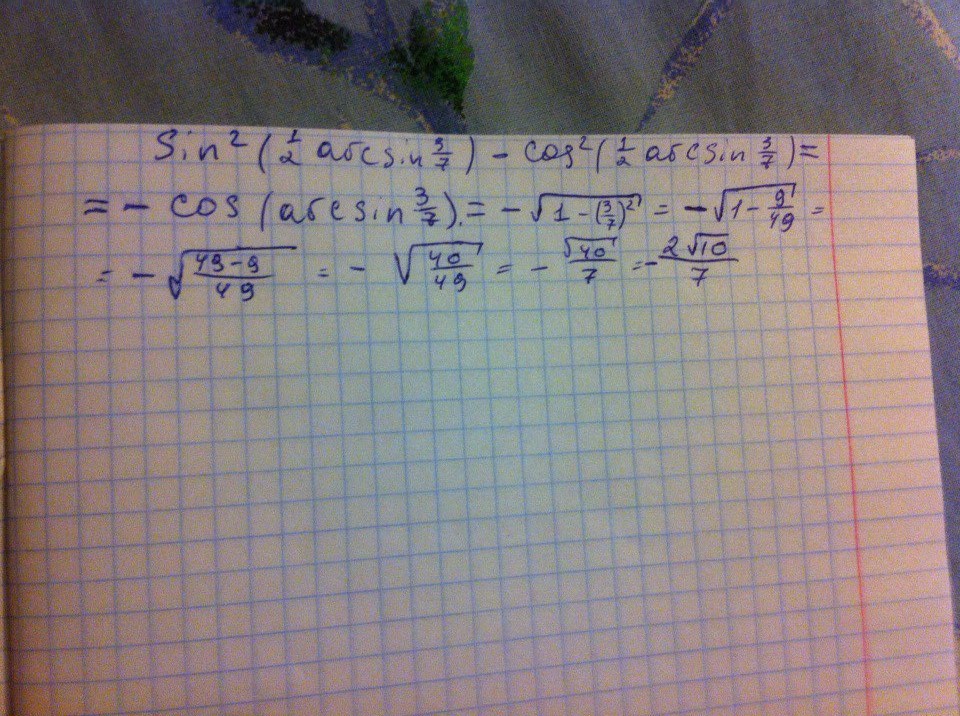
Автор ответа:
0
Если скажешь, что именно не понятно, я могу попробовать объяснить
Автор ответа:
0
напиши от руки
Автор ответа:
0
кидок(
Автор ответа:
0
Не заметил твоего сообщения)
Автор ответа:
0
Добавил фотку)
Похожие вопросы
Предмет: Психология,
автор: pavlunya666
Предмет: Қазақ тiлi,
автор: aluatulen12
Предмет: Русский язык,
автор: anastasia2009lyashev
Предмет: Математика,
автор: мася55
Предмет: Обществознание,
автор: darik199612