Question

В правильной треугольной пирамиде высота основания равна h, боковые ребра наклонены к основанию под углом альфа. Найти объем пирамиды.

Answer 1

В правильной треугольной пирамиде высота основания равна h, боковые рёбра наклонены к основанию под углом α. Найти объём пирамиды.

===========================================================

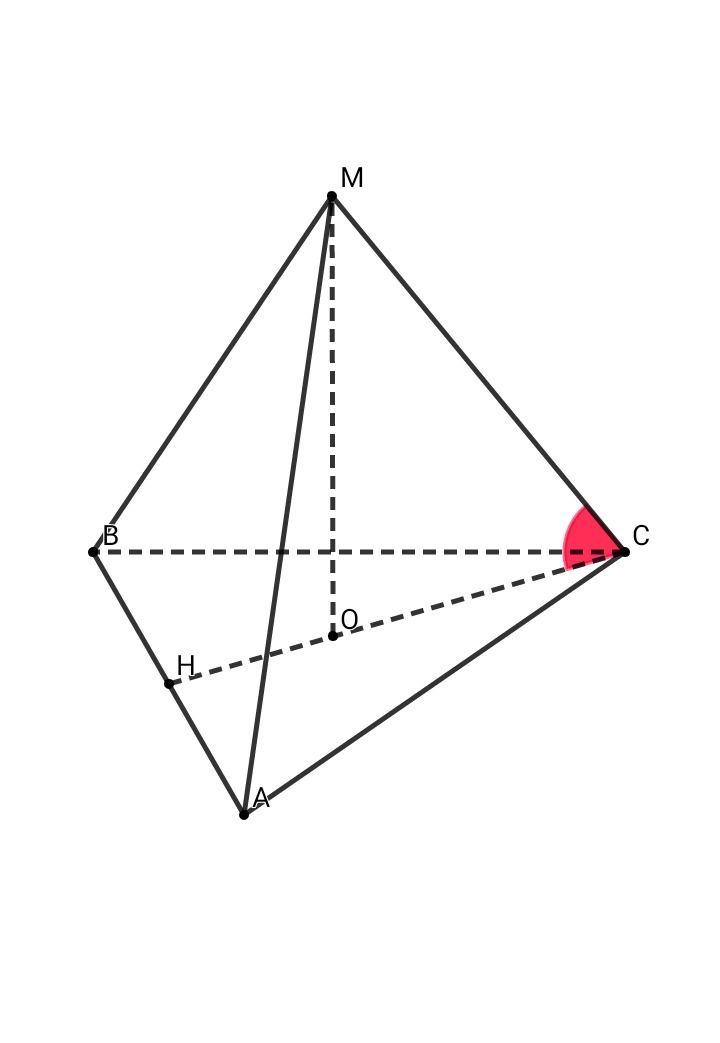
В основании правильной треугольной пирамиды лежит правильный треугольник. Вершина такой пирамиды проецируется в центр основания. Центр правильного треугольника является точка О - точка пересечения бисссектрис, медиан и высот.

СН = h , ∠ACB = α

В ΔАВС:  Медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1, считая от вершины.

СО:ОН = 2:1  ⇒  СО = 2•СН/3 = 2h/3

В ΔСАН:  sin60° = CH/AC  ⇒  AC = CH/sin60° = CH/(√3/2) = 2h/√3

В ΔСМО:  tgα = MO/CO  ⇒  MO = CO•tgα = 2h•tgα/3

V пир. = (1/3)•Sabc•MO = (1/3) • (AC²•√3/4) • MO = (1/3) • (2h/√3)² • (√3/4) • (2h•tgα/3) = 2√3•h³•tgα/27

ОТВЕТ: V = 2√3•h³•tgα/27