Question

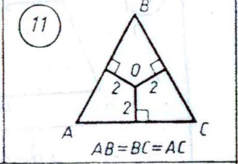
нужно найти площадь треугольника АВС

Answer 1

Здесь О - центр вписанной окружности. А треугольник АВС равносторонний, значит, его углы по 60 градусов. Если мы соединим точку О с вершинами треугольника, то получим 6 прямоугольных треугольников с одним углом в тридцать градусов (центр вписанной окружности лежит на точке пересечения биссектрис). Значит, другой острый угол у них по 60 градусов. Причём катет, противолежащий углам в тридцать градусов равен 2, а значит, гипотенуза равна 4. По теореме Пифагора находим, что второй катет равен $2 sqrt{2}$. Площадь такого маленького треугольничка - $2 sqrt{2}$. А площадь большого треугольника - это 6 площадей таких маленьких треугольничков, значит, площадь большого треугольника равна $12sqrt{2}$.

Ответ: $12 sqrt{2}$