Предмет: Алгебра,
автор: GenStaff
Ребят,помогите пожалуйста 3 и 4 номер
Приложения:
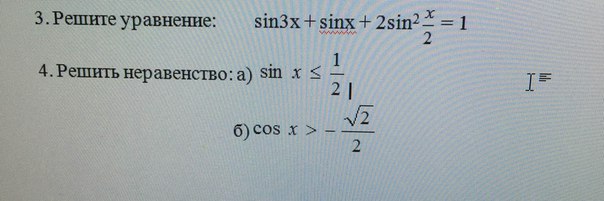
Ответы
Автор ответа:
0
3)



k∈Z

k∈Z
Ответ: k∈Z;
k∈Z;
 k∈Z.
k∈Z.
4)
a)

k∈Z
б)
 ,
,
k∈Z.
k∈Z
k∈Z
Ответ:
4)
a)
k∈Z
б)
k∈Z.
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Информатика,
автор: tibraeva09
Предмет: Қазақ тiлi,
автор: ussovanatalyaqz
Предмет: Биология,
автор: zvezda90000
Предмет: Алгебра,
автор: prasik2000