Предмет: Геометрия,
автор: kresina012
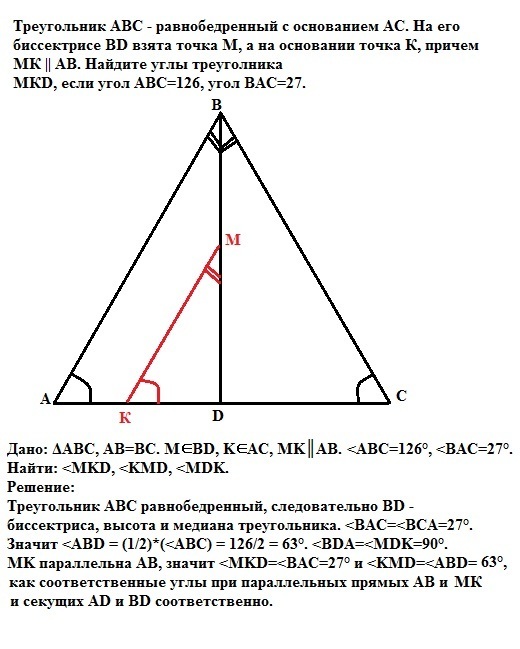
Треугольник АВС - равнобедренный с основанием АС. На его биссектрисе BD взята точка М, а на основании точка К, причем МК || АВ. Найдите углы треуголника
МКD, если угол АВС=126, угол ВАС=27.
Рисунок, дано, найти есть) Помогите только с решением..
Ответы
Автор ответа:
0
Дано: Треугольник АВС. АВ=ВСб М∈BD, K∈AC. MK║AB. <ABC=126°,<BAC=27°.
Найти <MKD, <KMD и <MDK.
Решение.
Треугольник АВС равнобедренный, следовательно BD - биссектриса, высота и медиана треугольника. <BAC=<BCA=27°, Значит
<ABD = (1/2)*(<ABC) = 126/2 = 63°. <BDA=<MDK = 90°.
MK параллельна АВ, значит <MKD=<BAC=27°, а <KMD=<ABD=63°, как соответственные углы при параллельных прямых АВ и МК и секущих AD и BD соответственно.
Ответ: <MKD=27°, <KMD=63°, <MDK=90°.
Приложения:
Похожие вопросы
Предмет: История,
автор: misagin1954
Предмет: Математика,
автор: sonechkak2010
Предмет: Математика,
автор: vkristinalebediva12
Предмет: Биология,
автор: Аноним
Предмет: География,
автор: Dinarka2126