Предмет: Алгебра,
автор: Liyaa
Помогите, пожалуйста.
Приложения:
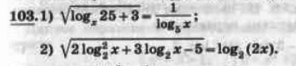
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Информатика,
автор: levleverov
Предмет: Геометрия,
автор: mila745
Предмет: Биология,
автор: aiym2009z
Предмет: География,
автор: Карина200029