1.Периметр квадрата, вписанного в окружность, равен 48см. НАйдите сторону правильного пятиугольника,вписанного в ту же окружность.
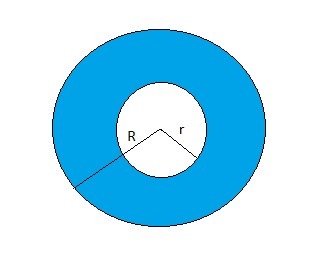
2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см
3.Найдите плозадь фигуры, ограниченной дугой окружности и стягивающей её хордой, если длина хорды равна 4м, а градусная мера дуги равна 60 градусов
Ответы
1. Общая формула для выражения радиуса описанной окружности R через сторону правильного n-угольника a:
Тогда для квадрата:
а для правильного пятиугольника:
Т.к. радиус окружности не изменяется, то можем записать:
Ответ: сторона правильного пятиугольника, вписанного в ту же окружность примерно 39,9 см
2. Площадь кольца ограниченного двумя концентрическими окружностями равна разности площадей большей и меньшей окружности.
Если обозначить радиус большей окружности через R, а меньшей окружности через r, то площадь кольца равна:
Ответ: площадь кольца, ограниченного двумя окружностями равна 40π см²
3. Площадь фигуры, ограниченной дугой окружности и стягивающей её хордой равна разности площадей сектора OAB и треугольника OAB.
ΔOAB равнобедренный с углом при вершине 60°, следовательно углы при основании равны (180° - 60°) / 2 = 60°. Т.е. ΔOAB - равносторонний и радиус окружности R = OA = AB = 4 м.
Площадь равностороннего треугольника выражается через его сторону по формуле:
Площадь сектора круга через угол α стягивающей его дуги и радиус окружности R найдем по формуле:
Площадь заданной фигуры равна:
Ответ: Площадь фигуры, ограниченной дугой окружности и стягивающей её хордой примерно 1,45 м²