Предмет: Геометрия,
автор: Лана141999
В окружность вписан правильный четырехугольник, и вокруг этой окружности описан правильный четырехугольник.Найдите отношения периметров и площадей этих четырехугольников.
Ответы
Автор ответа:
0
Смотрите вложенный файл. Там чертеж.
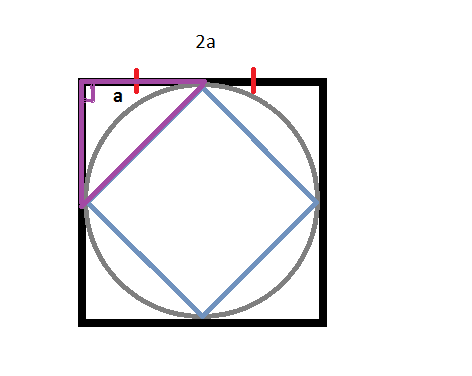
Допустим,около окружности описан квадрат(правильный четырехугольник),а в окружность вписан квадрат так,что вершины квадрата совпадают с точками касания окружности и описанного квадрата. (на чертеже все видно!)
Сторона описанного квадрата равна 2а. В точке касания она делится пополам,и эти "половинки" равны а.
Образуется прямоугольный треугольник. Из него получаем:
а²+а²=2а²
Тогда сторона вписанного квадрата равна а√2
Периметр вписанного квадрата равен p=4а√2
Периметр описанного квадрата равен P=8а
p/P=(4а√2)/(8а)=√2/2(это отношение периметров)
Площадь вписанного квадрата s=(a√2)²=2a²
Площадь описанного квадрата S=S₂=(2a)²=4a²
Отношение площадей:
s/S=(2a²)/(4a²)=1/2
Ответ: √2/2;1/2
Допустим,около окружности описан квадрат(правильный четырехугольник),а в окружность вписан квадрат так,что вершины квадрата совпадают с точками касания окружности и описанного квадрата. (на чертеже все видно!)
Сторона описанного квадрата равна 2а. В точке касания она делится пополам,и эти "половинки" равны а.
Образуется прямоугольный треугольник. Из него получаем:
а²+а²=2а²
Тогда сторона вписанного квадрата равна а√2
Периметр вписанного квадрата равен p=4а√2
Периметр описанного квадрата равен P=8а
p/P=(4а√2)/(8а)=√2/2(это отношение периметров)
Площадь вписанного квадрата s=(a√2)²=2a²
Площадь описанного квадрата S=S₂=(2a)²=4a²
Отношение площадей:
s/S=(2a²)/(4a²)=1/2
Ответ: √2/2;1/2
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: myr4ik28
Предмет: Математика,
автор: rjhheehejej
Предмет: Математика,
автор: bezumnoscastliwa
Предмет: Химия,
автор: LudimaSerebro