Предмет: Геометрия,
автор: ikhaliov
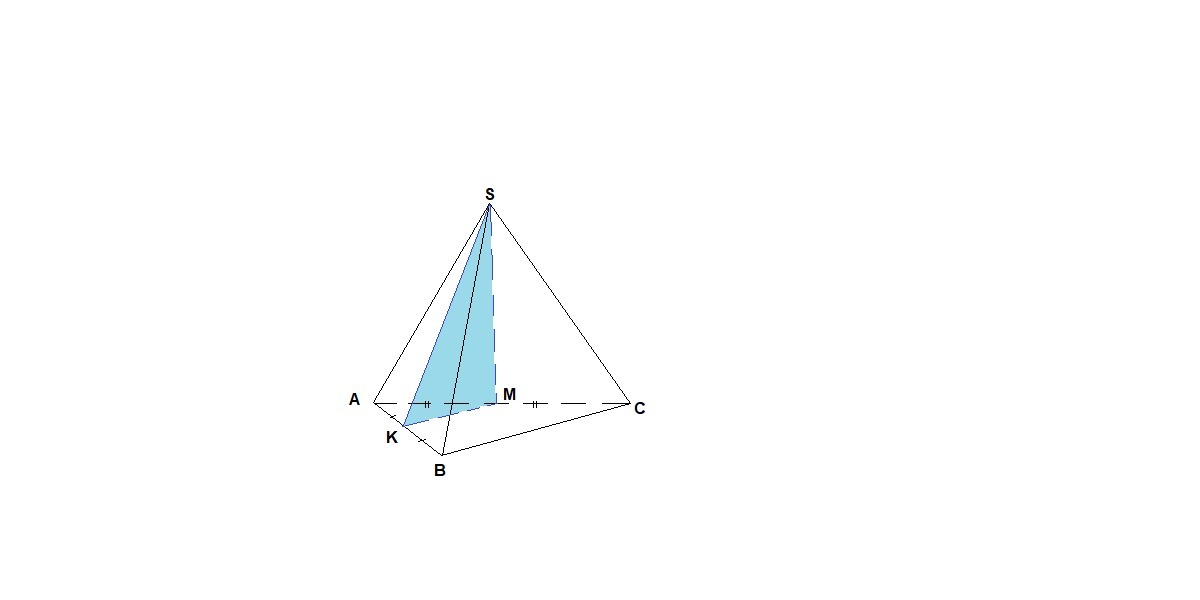
От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Ответы
Автор ответа:
0
КМ - средняя линия основания.
SAKM - отсеченная пирамида.
Vsabc = 12
Vsabc = 1/3 Sabc · h
Vsakm = 1/3 Sakm · h, так как эти пирамиды имеют общую высоту.
Рассмотрим треугольники АВС и АКМ:
АК : АВ = 1 : 2
АМ : АС = 1 : 2
угол при вершине А общий, значит треугольники подобны по двум пропорциональным сторонам и углу между ними.
k = 1/2
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sakm : S abc = 1 : 4
Sakm = 1/4 Sabc
Vsakm = 1/3 · 1/4 Sabc · h = 1/4 (1/3 Sabc · h) = 1/4 Vsabc
Vsakm = 1/4 · 12 = 3
Приложения:
Похожие вопросы
Предмет: Математика,
автор: 0996555375061
Предмет: Математика,
автор: minulinadamira40
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: v5i7t2a4
Предмет: Математика,
автор: azvlad0