Question

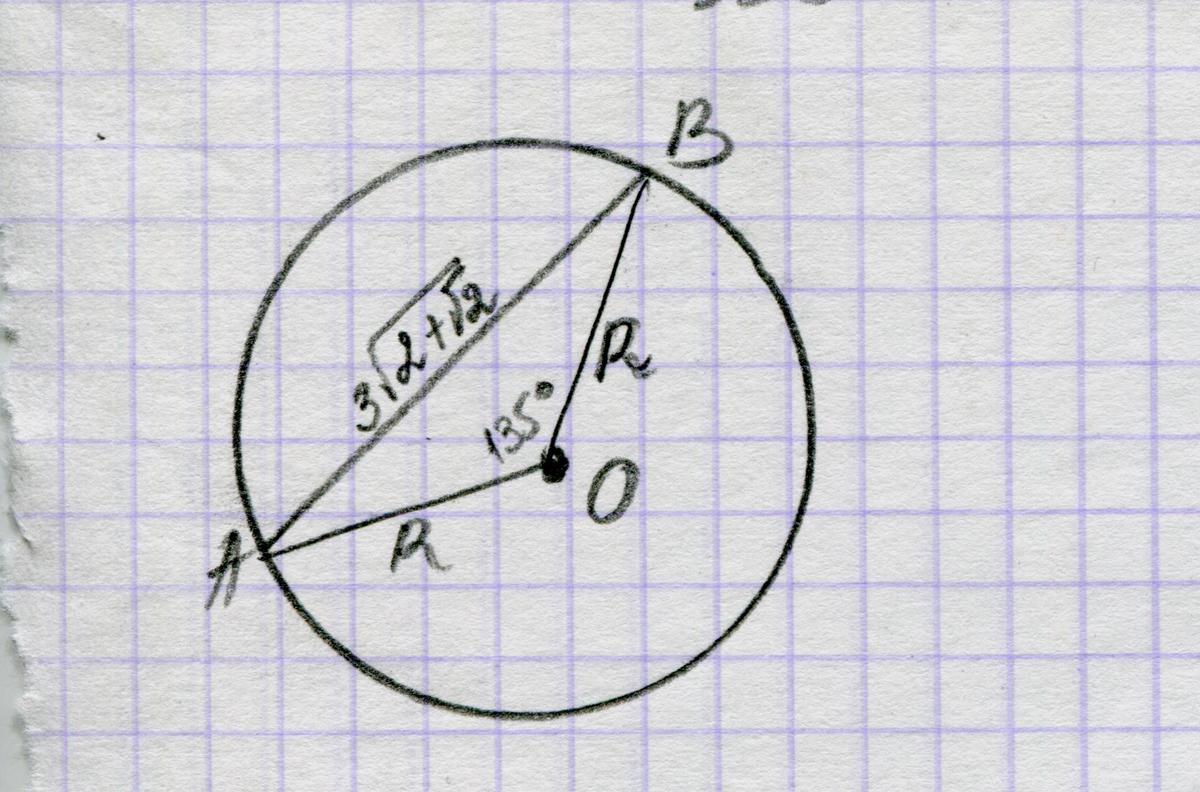
Хорда длиной 3√(2+√2) см. стягивает дугу градусная мера которой 135. Найти площадь кругового сектора соответствующего этой дуге?

Answer 1

применим теорему косинусов:
а²=в²+с²-2*в*с*cosА
(3√(2+√2))²=R²+R²-2*R*R*cos135
9(2+√2)=2R²-2R²cos135
9(2+√2)=2R²-2R²(-(√2/2))   
cos135=-cos(180-45)=-cos45=-(√2/2)
9(2+√2)=2R²+R²√2  
9(2+√2)=R²(2+√2)
  9=R²
R=3
S(сектора)=(πR²α)/360
S=(π*9*135)/360= сокращаем = (135π)/40 =(27π)/8