Question

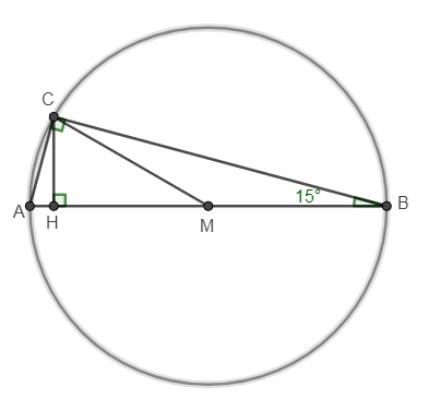
В прямоугольном треугольнике ABC угол B равен 15 градусов Из вершины прямого угла C проведены высота CH и медиана CM. Найдите отношения CH : AB и MH:BC

Answer 1

1). Построим описанную окружность с центром в т. М
     Угол ∠АМС - центральный, опирающийся на ту же дугу АС,
     что и угол ∠АВС.
     Следовательно:   ∠АМС = 2*∠АВС = 2*15 = 30°

     В ΔМНС:  CH = MC*sin30° = MC/2

     Так как АВ = 2*МС, то: СН:АВ = МС/2 : 2MC = 1/4
                                           CH:AB = 1:4 

2). В ΔАВС:    cos∠ABC = BC/AB = BC/2MC  =>
                                        => BC = 2MC*cos15°
   
     В ΔМНС:   МН = МС*cos30° = MC*√3/2
                                  
Тогда:  $displaystyle MH:BC= frac{2MC*cos15}{MC* sqrt{3}/2}= frac{4cos15}{ sqrt{3}}= frac{4 sqrt{3}}{3}cos15$