Question

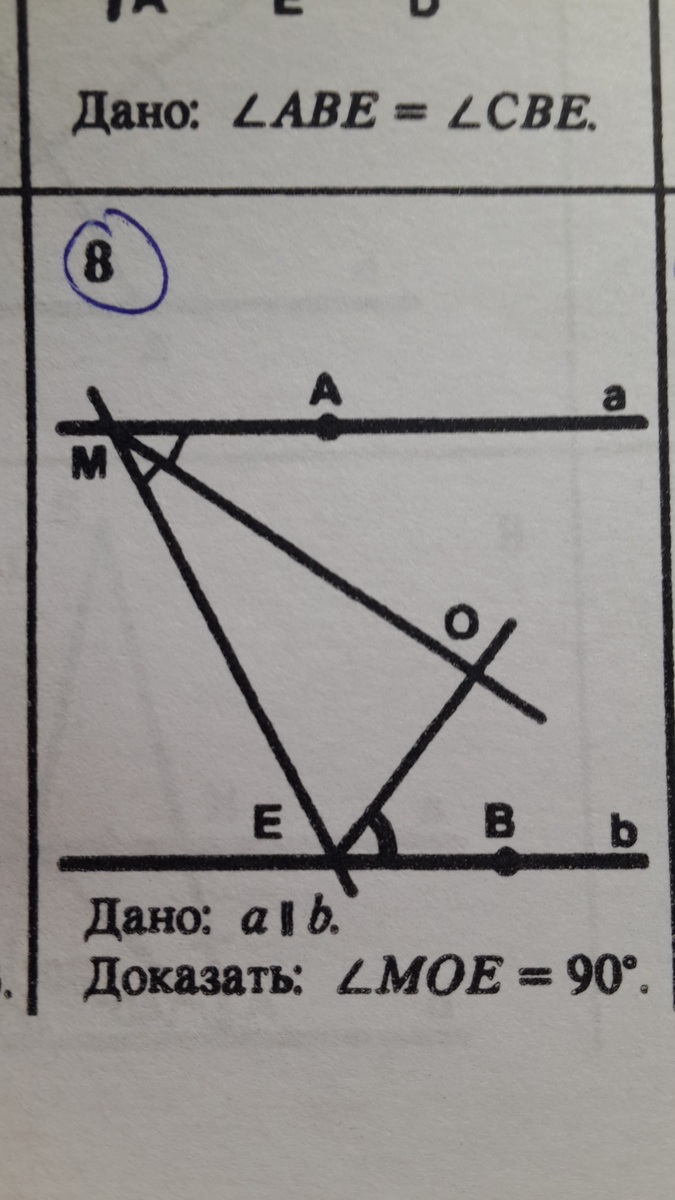
Помогите с геометрией. Дано: a||b
Доказать: Угол MOE=90 градусов.
Зараннее спасибо!

Answer 1

На чертеже ошибка: луч ЕО должен быть биссектрисой угла МЕВ.

∠АМЕ + ∠МЕВ = 180° так как это внутренние односторонние углы при пересечении параллельных прямых а и b секущей МЕ.

МО - биссектриса ∠АМЕ, значит

∠АМЕ = 2∠ОМЕ.

ЕО - биссектриса ∠МЕВ, значит

∠МЕВ = 2∠ОЕМ.

Итак,

2∠ОМЕ + 2∠ОЕМ = 180°

2 (∠ОМЕ + ∠ОЕМ) = 180°

∠ОМЕ + ∠ОЕМ = 90°

Сумма углов треугольника равна 180°.

ΔОМЕ:

∠МОЕ = 180° - (∠ОМЕ + ∠ОЕМ) = 180° - 90° = 90°

Answer 2

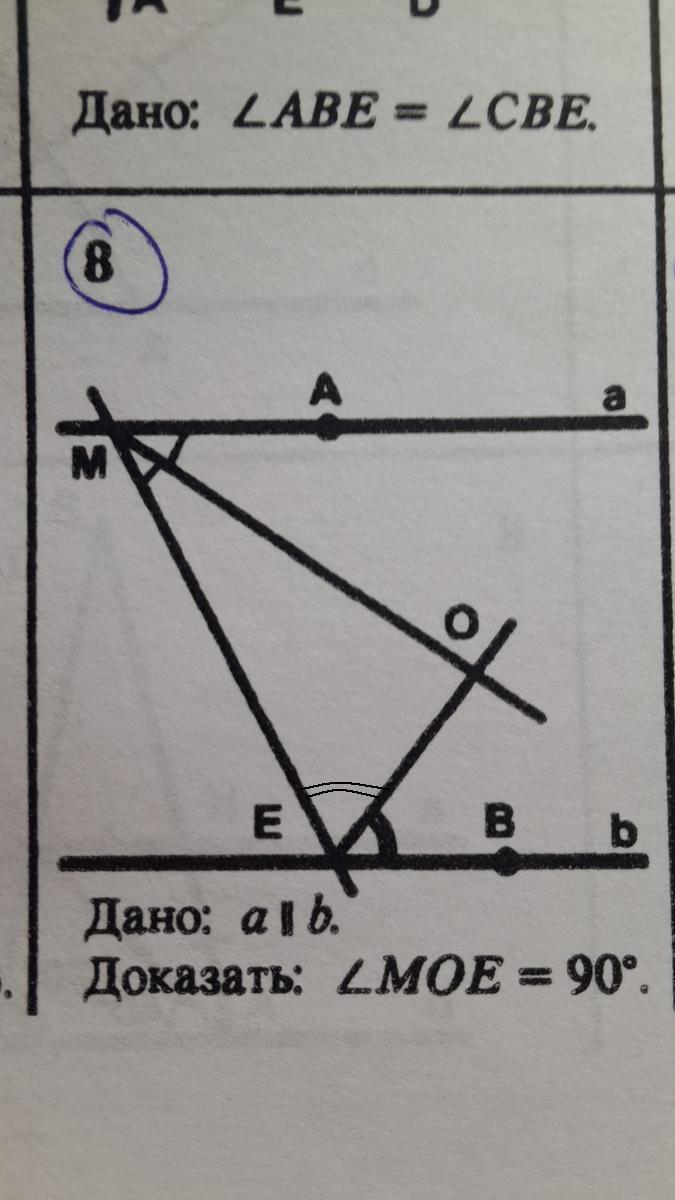
Т.к. a || b, то ∠АМЕ + ∠МЕВ = 180°, т.к. эти углы - односторонние (по свойству односторонних углов при параллельных прямых).

МО и ЕО - биссектрисы этих углов (см. рис.), т.е. делят их пополам, тогда

∠ОМЕ + ∠МЕО = 90°.

Т.к. сумма углов любого треугольника равна 180°, то

∠ОМЕ + ∠МЕО + ∠МОЕ = 180°, откуда ∠МОЕ = 180° - (∠ОМЕ + ∠МЕО) =

= 180° - 90° = 90°.