Question

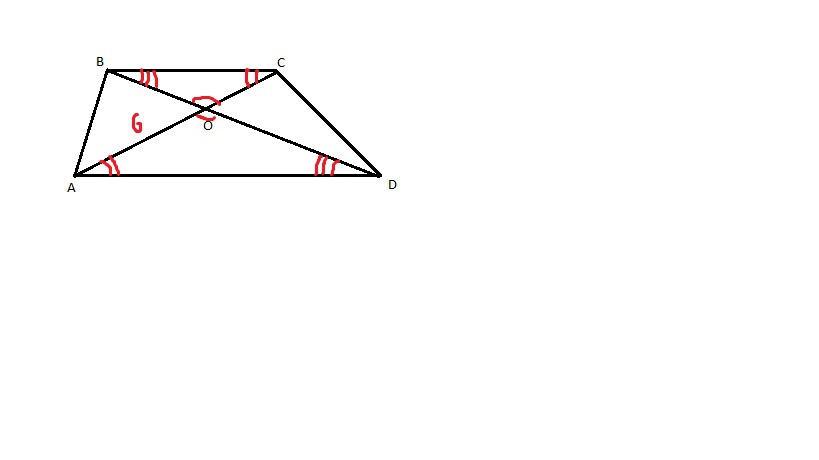
В трапеции ABCD (BC и AD - параллельны) диагонали пересекаются в точке О. Площадь треугольника ВОС равна 3, а площадь треугольника AOD равна 27. Найдите АС, если АО = 6

Answer 1

Из трапеции АВСD имеем: углы ВОС и АОD равны как вертикальные, углы ОАD и ОСВ, а также углы ODA и ОВС равны как внутренние разносторонние. Следовательно, треугольники BOC и AOD подобны по трем углам. Из теоремы подобных треугольников: отношение площадей подобных треугольников равно квадрату коэффициенту их подобия, то есть S(AOD)/S(BOC) = k^2. Имеем: k^2 = 27/3, k^2 = 9, k = 3. Стороны подобных треугольников пропорциональны: AO/OC = k, имеем: 6/OC = 3, OC = 6/3, OC = 2. АС = АО + ОС, АС = 6 + 2 = 8.
Ответ: 8.