Расстояние между непересекающимися диагоналями вух смежных боковых граней куба равно 2. Определить полную поверхность куба.
Ответы
наименьшее расстояние между этими диагоналями будет расстояние между центрами этих диагоналей.
Далее, можно рассуждать следующим образом:
Построим аналогичные диагонали на 2 других зеркальных данным граням, проведем такие же прямые (соединящие эти грани) и посмотрим на куб сверху. Увидим следующее (рисунок в приложении).
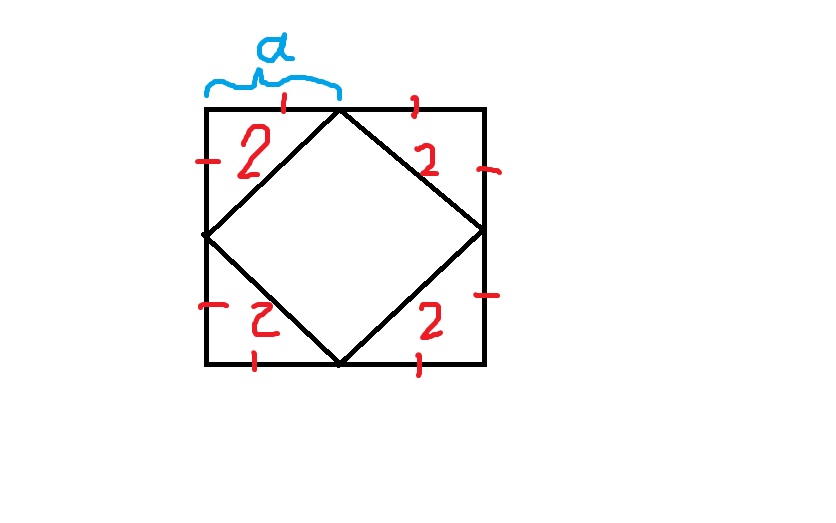
У нас внутри исходного квадрата (это вертикальная проекция куба), появился вписанный в него маленький квадрат, образованный расстояниями между диагоналями. Стороны этого квадрата равны 2. И сам маленкьий квадрат делит проекцию исходного куба (которая тоже является квадратом пополам.)
собственно, дальше задача сводится к свойствам прямоугольного треугольника, у которого гипотенуза 2, а катеты (равные половине сторон большого квадрата будут равны а).
дальше по теореме Пифагора.
а^2+a^2=4
a=корень из 2
тогда сторона большого квадрата будет равна 2*2^(1/2) т.е. два умножить на корень из двух.
А объем исходного куба - это значение в 3 степени
или
16 умножить на корень из 2