Пожалуйста, решите хотя бы одну. И если можно распишите решение.
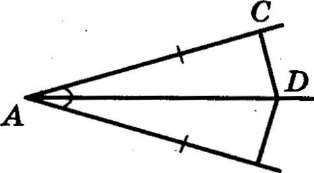
1. На сторонах угла ВАС равного 20 град. и на его биссектрисе отложены равные отрезки АВ, АС, и АD. Определите величину угла ВDС.
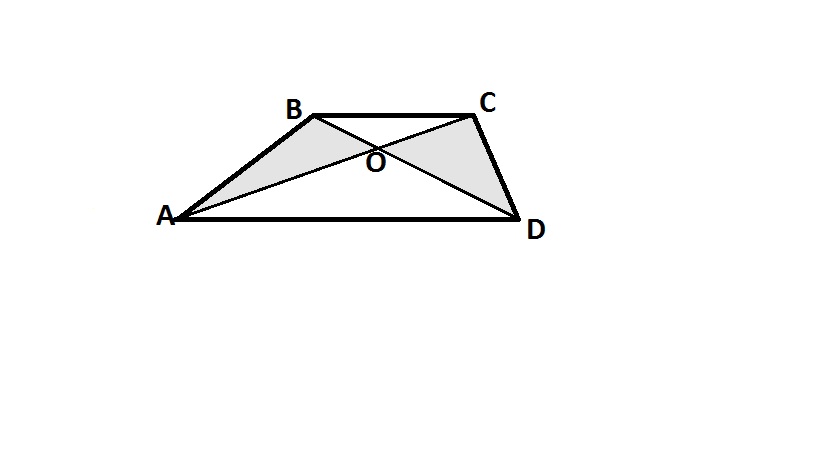
2. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O.Докажите, что площади треугольников AOB и COD равны.
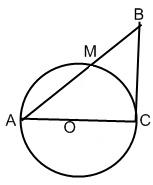
3.Длина катета AC прямоугольного треугольника ABC равна 8 см. Окружность с диаметром AC пересекает гипотенузу AB в точке M. Найдите площадь треугольника ABC, если известно, что AM : MB = 16 : 9.
Ответы
1
Ответ
L BAD = L DAC = L A/2 = 20/2 = 10 град.
В треугольниках ABD и ADC:
AB = AD
AD = AC =>
треугольники равнобедренные => углы при BD и DC равны:
(180 - 10)/2 = 170/2 = 85 град. =>
L BDC = L ADB + L ADC = 2*L ADB = 2*85 = 170 град.
2
треугольник ABD= треугольник ACD - если у єтих треугольников общее основание AD, тогда высоты треугольников проведенные к основанию являются высотами трапеции и поетому равны:
треугольник AOB= треугольник ABD- треугольник AOD
треугольник COD= треугольник ACD- треугольник AOD
поєтому
треугольник AOB= треугольник COD.
Доказано!
3
Окружность пересекает гипотенузу и касается второго катета. Гипотенуза является секущей, а второй катет касательной, тогда справедливо равенство ВС^2=BM*AB (1)
AM=16x, BM=9x, AB=25x, BC^2=AB^2-AC^2, BC^2=625x^2-64. Подставляем все данные в равенство (1)
625x^2-64=25x*9x
625x^2-225x^2=64
400x^2=64
x^2=0,16
x=0,4 см
AB=10 см
BC=6 см
S=1/2*AC*BC, S=1/2*8*6=24 кв.см.
1)угол ДСА=90 градусов, угол САД=20:2=10 градусов, следовательно, угол СДА=90-10=80 градусов.
Угол СДА=углу ВДА=80 градусов, значит угол ВДА=80+80=160 градусов.