Предмет: Геометрия,
автор: max368
Помогите решить задачи
Приложения:
Ответы
Автор ответа:
0
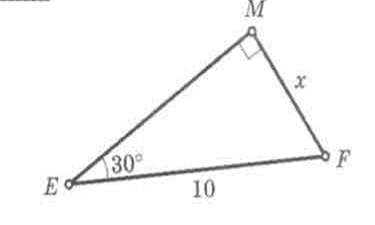
1.
х=5
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
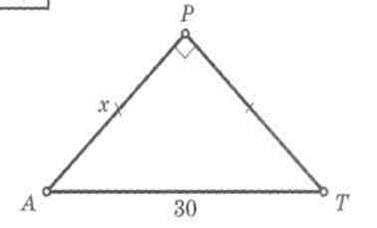
2.
По теореме Пифагора
х²+х²=30²
2х²=900
х²=450
х=15√2
или
острые углы треугольника 45°
х = 30·sin 45° = 30·(√2/2) = 15√2
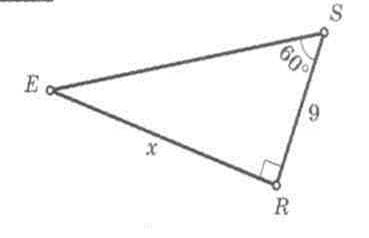
3.
х = 9·tg 60° = 9√3
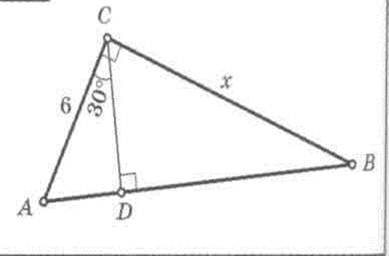
4.
∠A=60°
x=6·tg 60°=6·√3
5.
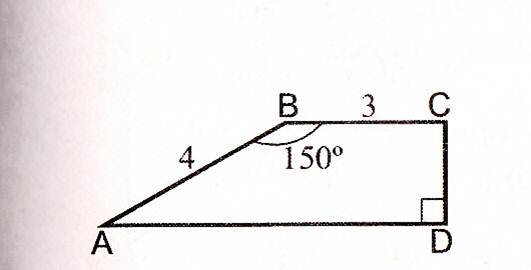
Проведем высоту ВН
∠А=30° ( сумма углов прилежащих к стороне АВ равна 180°)
ВН=CD=2 ( катет против угла в 30°)
АН=2·ctg 30°=2√3
HD=3
AD=3+2√3
х=5
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
2.
По теореме Пифагора
х²+х²=30²
2х²=900
х²=450
х=15√2
или
острые углы треугольника 45°
х = 30·sin 45° = 30·(√2/2) = 15√2
3.
х = 9·tg 60° = 9√3
4.
∠A=60°
x=6·tg 60°=6·√3
5.
Проведем высоту ВН
∠А=30° ( сумма углов прилежащих к стороне АВ равна 180°)
ВН=CD=2 ( катет против угла в 30°)
АН=2·ctg 30°=2√3
HD=3
AD=3+2√3
Похожие вопросы
Предмет: Английский язык,
автор: tanadmitrienko69
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Информатика,
автор: nastya211196
Предмет: География,
автор: ageevaelizavet1