Предмет: Геометрия,
автор: HappyParovozik
Основание пирамиды правильный треугольник со стороной 6.
Одно из боковых рёбер перпендикулярно к основанию, а два других наклонены к плоскости основания под углом 30 градусов.Найдите объем призмы.
Ответы
Автор ответа:
0
Из правильного треугольника АВС: из теоремы Пифагора: высота ВК равна 3 корня из 2. Угол ОАК - это угол между плоскостью АОС и основанием. Поскольку угол ОАК = 30 градусов, то катет ОК равен гипотенузы ОА как катет, который лежит против угла 30 градусов. ОК = ОА/2. Пускай ОК = х, тогда ОА = 2х. Из прямоугольного треугольника ОАК: за теоремой Пифагора: OA^2 = OK^2 + AK^2, 4x^2 = 9 - x^2, 3x^2 = 9, x^2 = 3, x = корень из 3. OK = корень из 3. Объем призмы равен площади основания умножить на высоту: S = So*H = S(ABC)*OK = BK*AC/2*OK = 9 корней из 6.
Приложения:
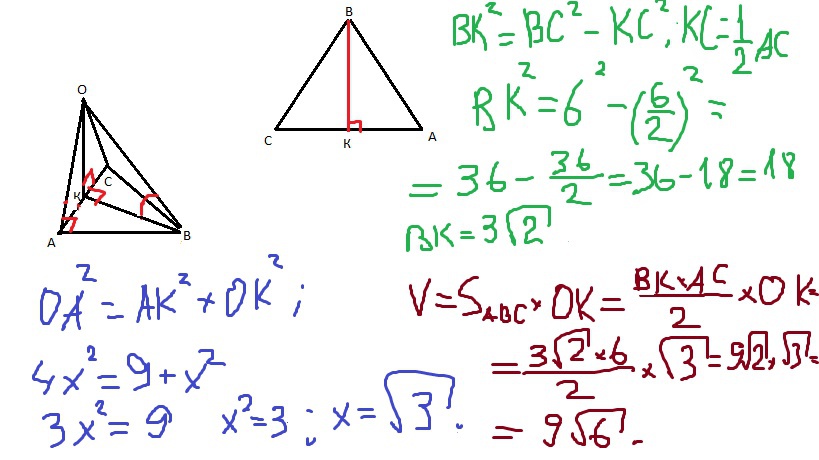
Автор ответа:
0
У вас же получилась грань перпендикулярна основанию, а в условии написано, что всего лишь ребро
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: dsaadasd
Предмет: Литература,
автор: ivanpismennij68
Предмет: Математика,
автор: Лесюнька2
Предмет: Математика,
автор: даринаа1029