Предмет: Геометрия, автор: Аноним

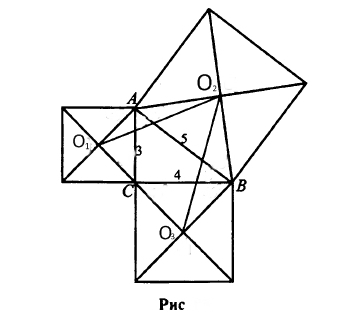
На сторонах треугольника внешним образом построены квадраты. Найдите площадь треугольника, вершинами которого являются центры этих квадратов(О1,02 И О3), если стороны треугольника равны 3, 4 и 5.

Приложения:

Ответы

Автор ответа: nelle987

Из рисунка (см. вложение) более-менее очевидно, что O2C - биссектриса прямого угла ACB (симметрия налицо). А т.к. углы АСО1, ВСО3 по 45 градусов, то О2С - высота в треугольнике О1О2О3.

Дальше все ясно, искомая площадь равна 1/2*7/sqrt(2)*7/sqrt(2)=49/4.

Приложения:

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Геометрия, автор: anastasiakirienko3

решите геометрии одно задание
Найти решение

6 лет назад

Предмет: Математика, автор: o6konovtmemer

2. Выберите правильное равенство[1 балл]
3. А) 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 64
В) 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 46
С) 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4 ∙ 6
Д) 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4 : 6

помогите пж

6 лет назад

Предмет: Другие предметы, автор: ninayavaeva

Соотнеси картинки и способы ловли мяча на рисунке.

Ловля двумя руками мяча, летящего высоко

Ловля двумя руками мяча, летящего низко

Ловля двумя руками мяча, летящего на средней высоте

Назад

Проверить

6 лет назад

Предмет: Физика, автор: Аноним

Тело которое движется равноускоренно из состояния покоя,прошло 450 м за 6 с. С каким ускорением оно двигалось?На каком расстоянии оно будет находится через 4 с после начала движения?

9 лет назад

Предмет: Математика, автор: Рената2003

Мама испекла пирожки.Маша съела половину .Затем пришел Олег и тоже съел половину того, что осталось.Надя съела половину остатка сама,а остальное 1 пирожок отдала маме.Сколько пирожков испекла мама? Кто съел самое большое количество пирожков?

9 лет назад