Предмет: Алгебра,
автор: Annabell98
Решите показательные уравнения:
Приложения:
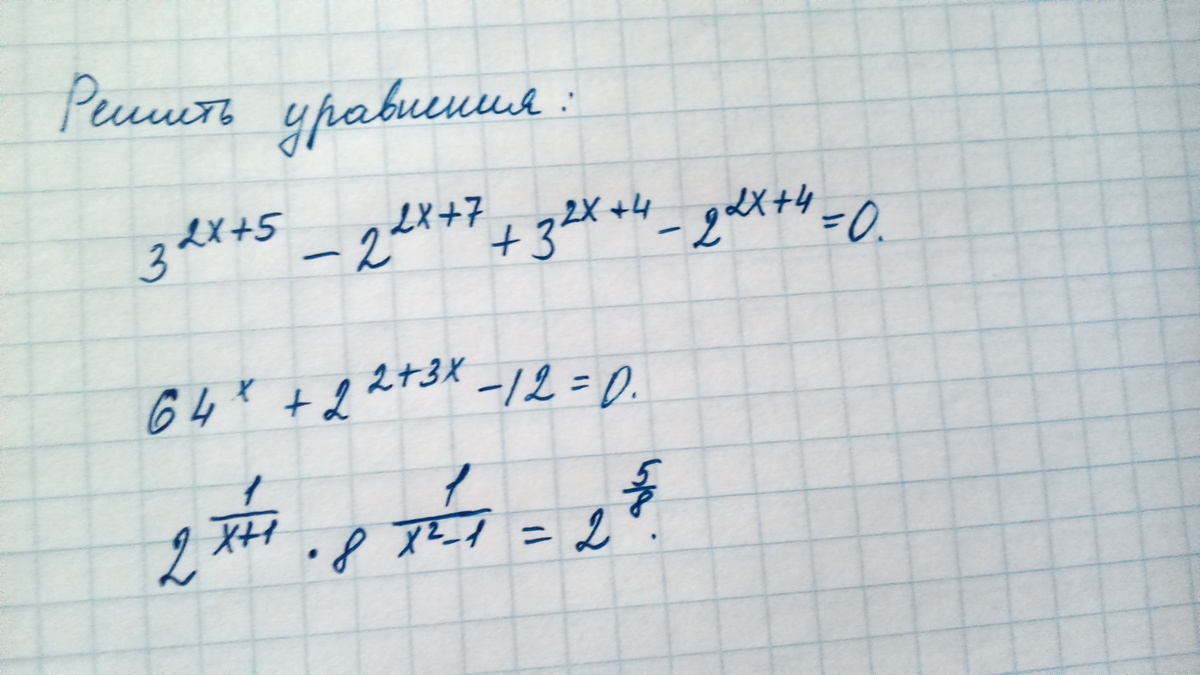
Ответы
Автор ответа:
0
64^x+2^(2+3x)-12=0
4^(3x)+2² *2^(3x)-12=0
(2²)^(3x)+4*2^(3x)-12=0
(2^(3x))²+4*2^(3x)-12=0 показательное квадратное уравнение.
замена переменных: 2^(3x)=t, t>0
t²+4t-12=0.
t₁=-6, -6<0. t=-6 посторонний корень
t₂=2
обратная замена:
t=2, 2^(3x)=2
2^(3x)=2¹. 3x=1. x=1/3
(2^(1/(x+1))) *(8^(1/(x²-1)))=2^(5/8)
2(1/(x+1))*((2³)^(1/(x²-1)))=2^(5/8)
2^((1/(x+1))+(3/(x²-1)))=2^(5/8)
1/(x+1)+3/(x²-1)=5/8 |* (8*(x²-1))
ОДЗ:
{x+1≠0 {x≠-1
x²-1≠0 x≠-1, x≠1
8(x-1)+24=5*(x²-1)
5x²-8x-21=0
x₁=-1,4. x₂=3
3^(2x+5)-2^(2x+7)+3^(2x+4)-2^(2x+4)=0
3^(2x)*3⁵+3^(2x)*3⁴=2^(2x)*2⁷+2^(2x)*2⁴
243*3^(2x)+81*3^(2x)=128*2^(2x)+16*2^(2x)
324*3^(2x)=144*2^(2x) | : 144*2^(2x)
324*3^(2x)/(144*2^(2x))=1
(324/144)*(3/2)^(2x)=1
(18/12)² *(3/2)^(2x)=1
(3/2)² *(3/2)^(2x)=1
(3/2)^(2+2x)=1
(3/2)^(2+2x)=(3/2)⁰
2+2x=0
x=-1
4^(3x)+2² *2^(3x)-12=0
(2²)^(3x)+4*2^(3x)-12=0
(2^(3x))²+4*2^(3x)-12=0 показательное квадратное уравнение.
замена переменных: 2^(3x)=t, t>0
t²+4t-12=0.
t₁=-6, -6<0. t=-6 посторонний корень
t₂=2
обратная замена:
t=2, 2^(3x)=2
2^(3x)=2¹. 3x=1. x=1/3
(2^(1/(x+1))) *(8^(1/(x²-1)))=2^(5/8)
2(1/(x+1))*((2³)^(1/(x²-1)))=2^(5/8)
2^((1/(x+1))+(3/(x²-1)))=2^(5/8)
1/(x+1)+3/(x²-1)=5/8 |* (8*(x²-1))
ОДЗ:
{x+1≠0 {x≠-1
x²-1≠0 x≠-1, x≠1
8(x-1)+24=5*(x²-1)
5x²-8x-21=0
x₁=-1,4. x₂=3
3^(2x+5)-2^(2x+7)+3^(2x+4)-2^(2x+4)=0
3^(2x)*3⁵+3^(2x)*3⁴=2^(2x)*2⁷+2^(2x)*2⁴
243*3^(2x)+81*3^(2x)=128*2^(2x)+16*2^(2x)
324*3^(2x)=144*2^(2x) | : 144*2^(2x)
324*3^(2x)/(144*2^(2x))=1
(324/144)*(3/2)^(2x)=1
(18/12)² *(3/2)^(2x)=1
(3/2)² *(3/2)^(2x)=1
(3/2)^(2+2x)=1
(3/2)^(2+2x)=(3/2)⁰
2+2x=0
x=-1
Автор ответа:
0
3^(2x+5) -2^(2x+7) +3^(2x+4) -2^(2x +4) ;
3^(2x+5)+3^(2x+4) =2^(2x+7) +2^(2x +4) ;
3^(2x+4)*(3 +1) =2^(2x +4)*(2³ +1) ;
3^(2x+4)*2² =2^(2x +4)*3² ;
(3/2)^(2x+4) =(3/2)² ;
2x+4 =2 ;
x = -1.
-------
64^x +2^(2+3x) -12=0 ; * * * 64^x =(8²)^x=8^2x =(8^x)² * * *
(8^x)² +2²*(2^3x) -12 =0 ;
(8^x)² +4*(8^x) -12 =0 ;
замена переменной: t =8^x > 0
t² +4t -12=0 ; * * * [ t =2 ; t = -6 * * *
t₁ = -6 < 0 →не решение исходного уравнения
t₂ =2⇒8^x =2⇔2^(3x) =2¹ ⇔3x =1⇔ x =1/3.
-------
( 2^1/(x+1) ) * (8 ^1/(x² -1) =2^(5/8) ;
* * * ОДЗ :x ≠ ± 1. ⇔ x∈( -∞; -1) U (-1;1) U(1;∞). * * *
2^(1/(x+1) + 3/(x² -1)) =2^(5/8) ;
1/(x+1) + 3/(x² -1) =5/8 ;
8(x-1 +3) =5(x² -1) ;
5x² -8x -21 =0 ;
x₁ =(4 -11)/5 = -7/5; * * *или иначе -1,4 * * *
x₂ =(4 +11)/5 = 3.
x₁ , x₂ ∈ ОДЗ.
ответ : -1,4 ; 3.
3^(2x+5)+3^(2x+4) =2^(2x+7) +2^(2x +4) ;
3^(2x+4)*(3 +1) =2^(2x +4)*(2³ +1) ;
3^(2x+4)*2² =2^(2x +4)*3² ;
(3/2)^(2x+4) =(3/2)² ;
2x+4 =2 ;
x = -1.
-------
64^x +2^(2+3x) -12=0 ; * * * 64^x =(8²)^x=8^2x =(8^x)² * * *
(8^x)² +2²*(2^3x) -12 =0 ;
(8^x)² +4*(8^x) -12 =0 ;
замена переменной: t =8^x > 0
t² +4t -12=0 ; * * * [ t =2 ; t = -6 * * *
t₁ = -6 < 0 →не решение исходного уравнения
t₂ =2⇒8^x =2⇔2^(3x) =2¹ ⇔3x =1⇔ x =1/3.
-------
( 2^1/(x+1) ) * (8 ^1/(x² -1) =2^(5/8) ;
* * * ОДЗ :x ≠ ± 1. ⇔ x∈( -∞; -1) U (-1;1) U(1;∞). * * *
2^(1/(x+1) + 3/(x² -1)) =2^(5/8) ;
1/(x+1) + 3/(x² -1) =5/8 ;
8(x-1 +3) =5(x² -1) ;
5x² -8x -21 =0 ;
x₁ =(4 -11)/5 = -7/5; * * *или иначе -1,4 * * *
x₂ =(4 +11)/5 = 3.
x₁ , x₂ ∈ ОДЗ.
ответ : -1,4 ; 3.
Похожие вопросы
Предмет: Алгебра,
автор: 25love20055you
Предмет: Литература,
автор: Hacker0999
Предмет: Литература,
автор: Sumbulat
Предмет: Алгебра,
автор: Lokomotiv7