Предмет: Геометрия,
автор: Anika004323444
в плоскости равнобедренного прямоугольника..
Приложения:

Ответы
Автор ответа:
0
Применено определение двугранного угла
Приложения:

Автор ответа:
0
спасибо большое)
Автор ответа:
0
Рассмотрим равнобедренный прямоугольный треугольник АВС: поскольку АВ - гипотенуза, то ВС = АС как катеты равнобедренного треугольника. Пускай ВС = АС = x см, тогда за теоремой Пифагора: AB^2 = BC^2 + AC^2, (12*sqrt(3))^2 = x^2 + x^2, 2x^2 = 144*3, 2x^2 = 432, x^2 = 216, BC = AC = 6*sqrt(6) (х равно 6 корней из 6). Из прямоугольного треугольника DCA: DA^2 = DC^2 + AC^2, DA^2 = 324 + 216 = 540, DA = 6*sqrt(15). Треугольник DAB - равнобедренный, поскольку проекции DB и DA равны. Найдем медиану DF из прямоугольного треугольника DFA (в равнобедренном треугольнике медиана является также и высотой): DA = 6*sqrt(15), FA = AB/2 = 6*sqrt(3), из теоремы Пифагора: DF^2 = DA^2 - FA^2, DF^2 = 540 - 108 = 432, DF = 12*sqrt(3) см.
Из прямоугольного треугольника CDF: синус угла CFD равен отношению противолежащего катета DC к гипотенузе DF: sin(<CFD) = DC/DF, sin(<CFD) = 18/12*sqrt(3), sin(<CFD) = sqrt(3)/2. Угол, синус которого равен sqrt(3)/2 (корень из 3 разделить на 2) равен 60 градусов. Угол CFD - искомый угол между плоскостями DAB и CAB. Ответ: 60 градусов.
Из прямоугольного треугольника CDF: синус угла CFD равен отношению противолежащего катета DC к гипотенузе DF: sin(<CFD) = DC/DF, sin(<CFD) = 18/12*sqrt(3), sin(<CFD) = sqrt(3)/2. Угол, синус которого равен sqrt(3)/2 (корень из 3 разделить на 2) равен 60 градусов. Угол CFD - искомый угол между плоскостями DAB и CAB. Ответ: 60 градусов.
Приложения:
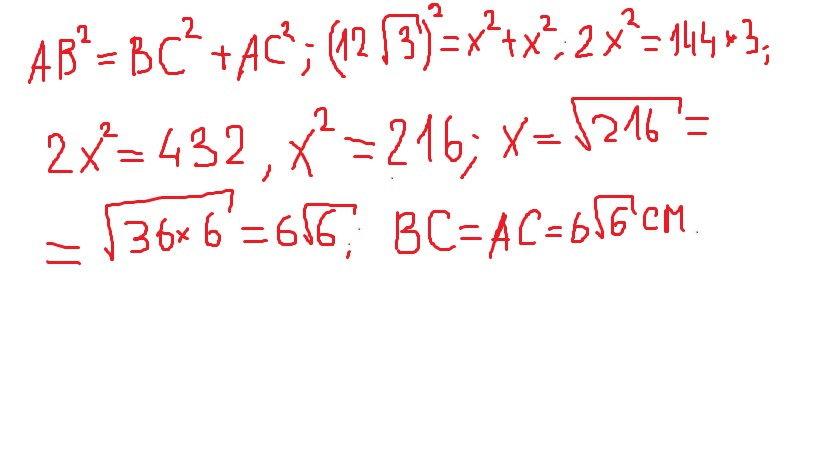
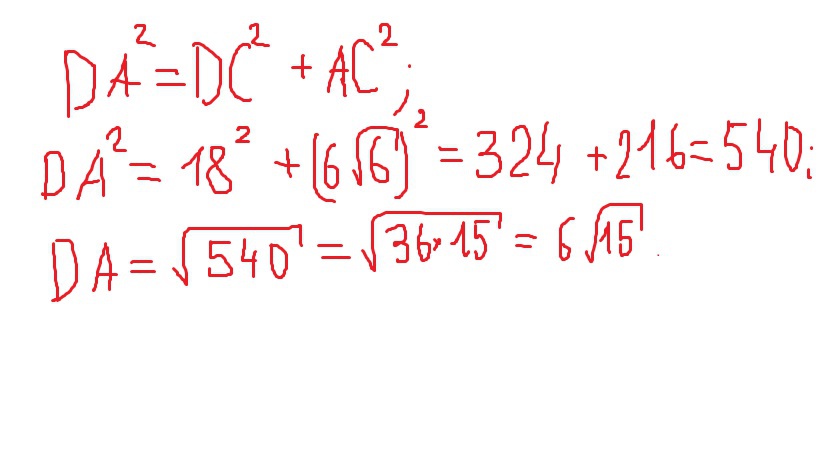

Автор ответа:
0
спасибо большое Вам)
Автор ответа:
0
А вам спасибо за интересно прошедшее время.
Похожие вопросы
Предмет: Математика,
автор: rokiyout
Предмет: Химия,
автор: nihatabdullaev9262
Предмет: История,
автор: arayka1708
Предмет: Математика,
автор: Tanya0205